Vestibular
Lista de questões resolvidas de função exponencial.
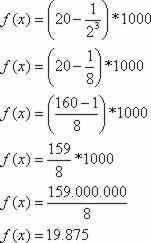 A população referente ao 3º ano é de 19.875 habitantes.
A população referente ao 3º ano é de 19.875 habitantes.
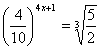
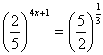
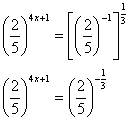
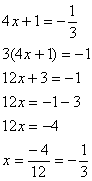 Resposta certa letra "A".
Resposta certa letra "A".
P(x) = P0 * (1 + i)t
6) Qual o domínio da função exponencial y = 2x ?
Resolução:
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Gráfico Da Função Do Primeiro Grau
Gráfico de Função do 1º grau Toda função pode ser representada graficamente, e a função do 1º grau é formada por uma reta. Essa reta pode ser crescente ou decrescente, dependendo do sinal de a. Quando a > 0 Isso significa que a será...
- Função Exponencial Teoria
A função exponencial é aquela na qual sua parte variável representada por x se encontra no expoente. Observe: y = 3 xy = 5 x + y = 0,9 xA lei de formação de uma função exponencial indica que a base elevada...
- Questões De Função Exponencial
Faça as seguintes questões de Função exponencial com gabarito e teste seus conhecimentos. Exercícios de Função exponencial 1) As funções y = ax e y = bx com a > 0 e b > 0 e a b têm gráficos que se interceptam em:...
- Questões Resolvidas De Progressão Aritmética
Lista de questões resolvidas sobre progressão aritmética de vestibulares anteriores. Exercícios resolvidos de P.A 1) Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, para que a soma...
Vestibular
Questões resolvidas de função exponencial
Lista de questões resolvidas de função exponencial.
1) (Fatec-SP - Adaptada) Suponhamos que a população de uma certa cidade seja estimada, para daqui a x anos, por 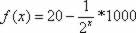 . Determine a população referente ao terceiro ano.
. Determine a população referente ao terceiro ano.
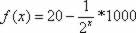 . Determine a população referente ao terceiro ano.
. Determine a população referente ao terceiro ano.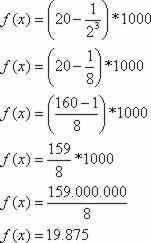 A população referente ao 3º ano é de 19.875 habitantes.
A população referente ao 3º ano é de 19.875 habitantes.2) (PUCC-SP) Numa certa cidade, o número de habitantes, num raio de r jm a partir do seu centro é dado por P(r) = k * 23r, em que k é constante e r > 0. Se há 98 304 habitantes num raio de 5 km do centro, quantos habitantes há num raio de 3 km do centro?
P(r) = k * 23r
98 304 = k * 2 3*5
98 304 = k * 215
98 304 = k * 32 768
k =98 304 / 32 768
k = 3
Calculando o número de habitantes num raio de 3 km
P (r) = k * 23r
P (3) = 3 * 23*3
P (3) = 3 * 29
P (3) = 3 * 512
P(3) = 1536
O número de habitantes num raio de 3 km é igual a 1536.
3) Se  , então "x" vale:
, então "x" vale:
a)  b)
b)  c)
c)  d)
d)  e)
e) 
Resolução:
Primeiro vamos transformar os decimais (números com vírgula) em frações:
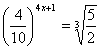
Veja que podemos simplificar a fração da esquerda e transformar em potência o lado direito da igualdade:
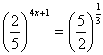
-As bases estão quase igualadas, só que uma é o inverso da outra. Vamos inverter uma delas e adicionar o expoente "-1".
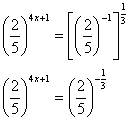
- Agora sim, com as bases igualadas podemos cortá-las:
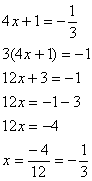 Resposta certa letra "A".
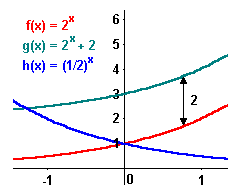
Resposta certa letra "A".4) A partir dos gráficos das funções f(x)=2x, g(x)=2x+2 e h(x)=2-x, descreva o que ocorre com g=g(x) e h=h(x) em relação a f=f(x).
Resolução:
O gráfico da função g(x)=2+2x é obtido de f(x)=2xtransladado verticalmente (no eixo y) por 2 unidades. O gráfico da função h(x)=(1/2)x é uma linha simétrica em relação ao eixo dos y (como se estivesse espelhada) que corresponde à função a f.
5) (EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,0320 = 1,80.
Resolução:
P(x) = P0 * (1 + i)t
P(x) = 500 * (1 + 0,03)20
P(x) = 500 * 1,0320
P(x) = 500 * 1,80
P(x) = 900
O PIB do país no ano de 2023 será igual a R$ 900 bilhões.
6) Qual o domínio da função exponencial y = 2x ?Sabemos que o domínio de uma função y = f(x) é o conjunto de valores que podem ser atribuídos a x. Observe que x sendo um expoente, ele poderá assumir qualquer valor e, portanto, o domínio da função dada é o conjunto dos números reais, ou seja:
D = R.
7) (IPA/IMEC) Se 2x+2-x=10 então 4x+4-x vale
Aplicando as propriedades de potenciação, o que o exercício dá e pede é:

- Este problema é o tipo de exercício que se você nunca viu como se faz, nunca iria conseguir fazer. Para resolvê-lo devemos pegar a equação dada e elevar ao quadrado ambos os lados. Veja só:
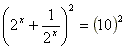
- Agora devemos efetuar ambos os lados. Não esqueça da regra para o produto notável da esquerda:
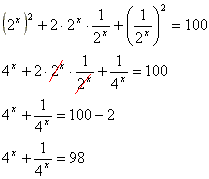 Resposta certa letra "D".
Resposta certa letra "D".
8) (ENEM-2009) Considere que uma pessoa decida investir uma determinada quantia e que lhe sejam apresentadas três possibilidades de investimento, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas:
a) M(t) = 24?t/75
b) M(t) = 24?t/50
c) M(t) = 25?t/50
d) M(t) = 25?t/150
Resolução
M(t) = 24 - t/75
v(10) = v0 * 2 ?0,2*10
12 000 = v0 * 2 ?2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
11) (UFCE ) Se f ( x ) = 16^(1+1/x), então f ( -1 ) + f ( -2 ) + f ( -4 ) é igual a :
a. 11
b. 13
c. 15
d. 17
e. nda
Resolução:
Outra questão simples .. basta calcular a função substituindo o x ....
f(-1) = 16^(1+1/-1)
f(-1) = 16^(1 - 1)
f(-1) = 16^0
f(-1) = 1 ...
f(-2) = 16^(1- 1/2)
f(-2) = 16^1/2 ....SEMPRE se lembre que denominador de expoente é raiz ... logo denominador 2 é raiz quadrada:
f(-2) = V16
f(-2) = 4 ...
f(-4) = 16^(1- 1/4)
f(-4) = 16^(3/4)
f(-4) = ?16³
f(-4) = 2³
f(-4) = 8 .... assim a soma vale
1 + 4 + 8 = 13 ...
Alternativa b.
12) Identifique o intervalo cujos valores de k tornam a função exponencial ,
,
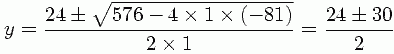
a) 4 b) 2 c) 0 d) -2 e) -4
Vamos desenhar o gráfico desta função: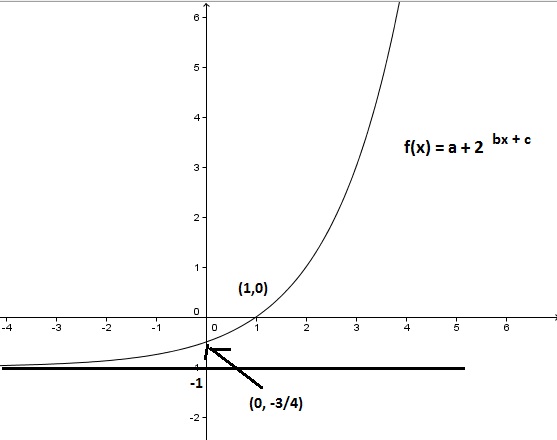
GANHE DINHEIRO ON LINE NO POSTMONEYS PARA SABER MAIS CLIQUE NO LINK ABAIXO:
www.superposts.com.br/pub.asp?cp=1598059

D = R.
7) (IPA/IMEC) Se 2x+2-x=10 então 4x+4-x vale
a) 40 b) 50 c) 75 d) 98 e) 100
Resolução:

- Este problema é o tipo de exercício que se você nunca viu como se faz, nunca iria conseguir fazer. Para resolvê-lo devemos pegar a equação dada e elevar ao quadrado ambos os lados. Veja só:
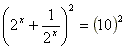
- Agora devemos efetuar ambos os lados. Não esqueça da regra para o produto notável da esquerda:
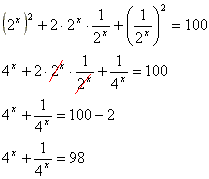 Resposta certa letra "D".
Resposta certa letra "D".8) (ENEM-2009) Considere que uma pessoa decida investir uma determinada quantia e que lhe sejam apresentadas três possibilidades de investimento, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas:
Investimento A: 3% ao mês
Investimento B: 36% ao ano
Investimento C: 18% ao semestre
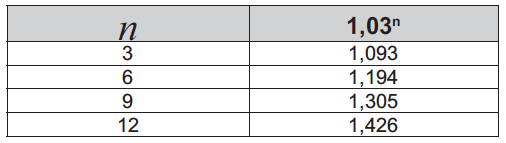
As rentabilidades, para esses investimentos, incidem sobre o valor do período anterior. O quadro fornece algumas aproximações para a análise das rentabilidades:

Para escolher o investimento com a maior rentabilidade anual, essa pessoa deverá
A) escolher qualquer um dos investimentos A, B ou C, pois as suas rentabilidades anuais são iguais a 36%.
B) escolher os investimentos A ou C, pois suas rentabilidades anuais são iguais a 39%.
C) escolher o investimento A, pois a sua rentabilidade anual é maior que as rentabilidades anuais dos investimentos B e C.
D) escolher o investimento B, pois sua rentabilidade de 36% é maior que as rentabilidades de 3% do investimento A e de 18% do investimento C.
E) escolher o investimento C, pois sua rentabilidade de 39% ao ano é maior que a rentabilidade de 36% ao ano dos investimentos A e B.
RESOLUÇÃO:
Galera, vamos calcular quanto vai render cada um dos investimentos.
? Investimento A: Rende 3% ao mês.
100% + 3% =103% = 1,03
Durante 12 meses teremos 1,0312 = 1,426 do valor inicial. (consulte a tabela)
? Investimento B: Rende 36% ao ano.
100% + 36% =136% = 1,36
Durante 1 ano teremos 1,36 do valor inicial.
? Investimento C: Rende 18% ao semestre.
100% + 18% =118% = 1,18
Durante 2 semestres teremos 1,182 = 1,3924 do valor inicial
Portanto, o investimento de maior rentabilidade no ano é o Investimento A.
Gabarito letra C.
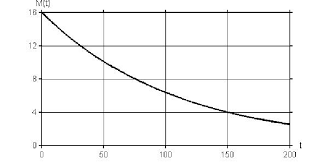
9) (Unicamp - 2011) Em uma xícara que já contém certa quantidade de açúcar, despeja-se café. A curva abaixo representa a função exponencial M(t), que fornece a quantidade de açúcar não dissolvido (em gramas), t minutos após o café ser despejado. Pelo gráfico, podemos concluir que

a) M(t) = 24?t/75
b) M(t) = 24?t/50
c) M(t) = 25?t/50
d) M(t) = 25?t/150
Resolução
- Para o ponto (0,16), temos:
- Para o ponto (150,4), temos:
M(t) = 24 - t/75
10) (Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v0 * 2 ?0,2t, em que v0 é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Resolução:
Resolução:
Temos que v(10) = 12 000, então:
v(10) = v0 * 2 ?0,2*10
12 000 = v0 * 2 ?2
12 000 = v0 * 1/4
12 000 : 1/ 4 = v0
v0 = 12 000 * 4
v0 = 48 000
A máquina foi comprada pelo valor de R$ 48 000,00.
a. 11
b. 13
c. 15
d. 17
e. nda
Resolução:
Outra questão simples .. basta calcular a função substituindo o x ....
f(-1) = 16^(1+1/-1)
f(-1) = 16^(1 - 1)
f(-1) = 16^0
f(-1) = 1 ...
f(-2) = 16^(1- 1/2)
f(-2) = 16^1/2 ....SEMPRE se lembre que denominador de expoente é raiz ... logo denominador 2 é raiz quadrada:
f(-2) = V16
f(-2) = 4 ...
f(-4) = 16^(1- 1/4)
f(-4) = 16^(3/4)
f(-4) = ?16³
f(-4) = 2³
f(-4) = 8 .... assim a soma vale
1 + 4 + 8 = 13 ...
Alternativa b.
12) Identifique o intervalo cujos valores de k tornam a função exponencial
f(x) = (5k ? 1)x decrescente.
A) 1/5 < k < 2/5
B) 0 < k < 1/5
C) k < 2/5
D) k > 1/5
E) k < 1
Resolução:
Para identificar o intervalo, devemos lembrar da seguinte propriedade da função exponencial:
Na função exponencial, cuja lei dada por f(x) = ax se 0 < a < 1, então a função é decrescente.
Veja, na lei de formação da função, a é a base da potência e deve estar entre 0 e 1 exclusivos.
Portanto, para que a função f do enunciado, dada pela lei f(x) = (5k ? 1)x seja decrescente, devemos ter
0 < 5k ? 1 < 1.
Resolvendo:
0 < 5k ? 1, então 1 < 5k, logo 1/5 < k.
5k ? 1 < 1, então 5k < 2, logo k < 2/5.
Logo, para que a função seja decrescente devemos ter 1/5 < k < 2/5.
13) Determinar o conjunto solução da equação 3x-34-x=24.
Resolução:
Como 34-x=34.3-x=81/3x, obtemos 3x-81/3x=24
Com a mudança de variável 3x=y, obteremos y-81/y=24
Multiplicando ambos os membros desta equação por y, obtemos a equação do segundo grau: y2-24y-81=0
Usando a fórmula quadrática, obtemos duas raízes reais
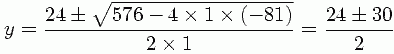
dadas por y1=27 e y2=-3 e como esta equação possui duas raizes reais, temos dois casos a considerar:
Caso 1: Se y1=27 então 3x=27=33, portanto x=3.
Caso 2: Se y2=-3 então 3x=-3. Como f(x)=3x é sempre positiva, esta função não pode assumir um valor negativo. Assim S={x em R: x=3}
14) (FUVEST-2013) Seja f(x) = a + 2^bx + c, em que a, b e c são números reais. A imagem de f é a semirreta ]-1, ?[ e o gráfico de f intercepta os eixos coordenados nos pontos (1,0) e (0,-3/4). Então o produto abc vale:
a) 4 b) 2 c) 0 d) -2 e) -4
Vamos desenhar o gráfico desta função:

Vamos analisar uma parte da função f(x). Iremos chamar a parte 2bx+ c de g(x).
A função g(x) = 2bx+ c tem a seguinte imagem:
Im g(x) = ]0, + ?[ , para todo x pertencente aos reais.
Mas a função f(x) tem uma constante ?a? somada com a função g(x). E a questão nos informa que o intervalo neste caso é:
Im f(x) = ]-1, + ?[
A soma de uma constante numa função exponencial faz com que ela se desloque sobre o eixo y (conjunto-imagem) e mude o valor do intervalo aberto à esquerda que será exatamente o da constante.
Na função f(x) temos a constante ?a? e o valor do intervalo aberto à esquerda é -1. Portanto, a = -1.
Já temos o valor de ?a?. Precisamos agora do valor de b e c.
A questão nos informa também que a função f(x) passa pelos pontos (1,0) e (0,-3/4).
Vamos ver o ponto (1,0):
Neste caso, temos x = 1 e y = f(1) = 0.
Logo,
f(x) = a+ 2bx+ c
f(1) = -1+ 2bx+ c
0 = -1 + 2b1+ c
-1 + 2b1+ c = 0
2b+ c = 20
b + c = 0
b = -c
Agora veremos o ponto (0,-3/4):
Neste caso, temos x = 0 e y = f(0) = -3/4.
Logo,
f(x) = a+ 2bx+ c
f(0) = -1+ 2bx+ c
-3/4 = -1 + 2b0+ c
1 ? 3/4 = 2c
1/4= 2c
2c = 1/4
2c = 2-2
c = -2
Mas b = -c. Logo, b = 2
Portanto, a = -1, b = 2 e c =-2
Logo, a.b.c = (-1).2.(-2) = 4
a.b.c = 4
ALTERNATIVA A
GANHE DINHEIRO ON LINE NO POSTMONEYS PARA SABER MAIS CLIQUE NO LINK ABAIXO:
www.superposts.com.br/pub.asp?cp=1598059

Seja sócio de nosso site, divida os lucros conosco, obtenha uma renda-extra usando a internet e ainda divulgue seu site gratuitamente!
mais informações no link:
http://www.anunciead.com/index.php?ref=cleitonp
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Gráfico Da Função Do Primeiro Grau
Gráfico de Função do 1º grau Toda função pode ser representada graficamente, e a função do 1º grau é formada por uma reta. Essa reta pode ser crescente ou decrescente, dependendo do sinal de a. Quando a > 0 Isso significa que a será...
- Função Exponencial Teoria
A função exponencial é aquela na qual sua parte variável representada por x se encontra no expoente. Observe: y = 3 xy = 5 x + y = 0,9 xA lei de formação de uma função exponencial indica que a base elevada...
- Questões De Função Exponencial
Faça as seguintes questões de Função exponencial com gabarito e teste seus conhecimentos. Exercícios de Função exponencial 1) As funções y = ax e y = bx com a > 0 e b > 0 e a b têm gráficos que se interceptam em:...
- Questões Resolvidas De Progressão Aritmética
Lista de questões resolvidas sobre progressão aritmética de vestibulares anteriores. Exercícios resolvidos de P.A 1) Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, para que a soma...