Vestibular
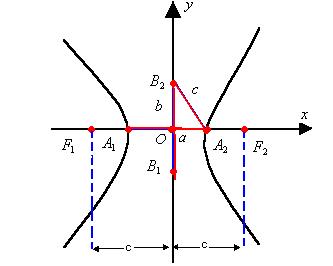
F1 e F2 ? são os focos da hipérbole
O ? é o centro da hipérbole
2c ? distância focal
2a ? medida do eixo real ou transverso
2b ? medida do eixo imaginário
c/a ? excentricidade
Existe uma relação entre a, b e c ? c2 = a2 + b2
Equação reduzida da hipérbole de eixo transverso horizontal
Obs: se o eixo transverso ou eixo real (A1A2) da hipérbole estiver no eixo dos y e o eixo não transverso ou eixo conjugado (B1B2) estiver no eixo dos x, a equação da hipérbole de centro na origem (0,0) passa a ser: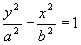
Hipérbole equilátera
É aquela em que a = b, ou seja, a medida do semi-eixo real é igual à medida do semi-eixo imaginário.
Cálculo da hipérbole equilátera
Sendo a = b
(eixo real sobre x) x² - y² = a²
(eixo real sobre y) y² - x² = a²
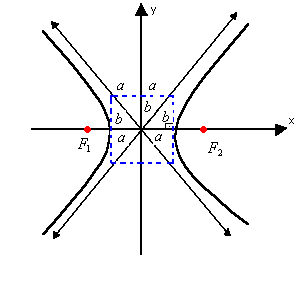
Exemplo: Determine a equação reduzida da hipérbole com eixo real 6, focos F1 (-5 , 0) e
F2 (5, 0).
Solução:
Temos que:
2a = 6 ? a = 3
F1(-5, 0) e F2(5, 0) ? c = 5
Da relação notável, obtemos:
c2 = a2 + b2 ? 52 = 32 + b2 ? b2 =25 ? 9 ? b2 = 16 ? b = 4
Assim, a equação reduzida será dada por:
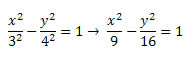
SOLUÇÃO:
Dividindo ambos os membros por 225, vem:
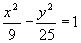
SOLUÇÃO:
Temos: 25x2 - 16y2 = 400. Observe que a equação da hipérbole não está na forma reduzida. Vamos dividir ambos os membro por 400. Fica então:
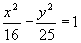
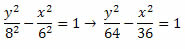
7) Mostre que a excentricidade de qualquer hipérbole equilátera é Ö 2.
Solução:
Como a = b e c² = a² + b², temos que c² = 2a², ou seja, c = Ö 2a.
Logo, e = c/a = Ö 2a/a = Ö 2
8) Encontre a equação da reta que passa pelo ponto P(2,3) e é perpendicular à reta que passa pelo centro da circunferência de equação x² + y² + 8x ? 4y + 11 = 0 e pelo foco de coordenadas positivas da hipérbole de equação
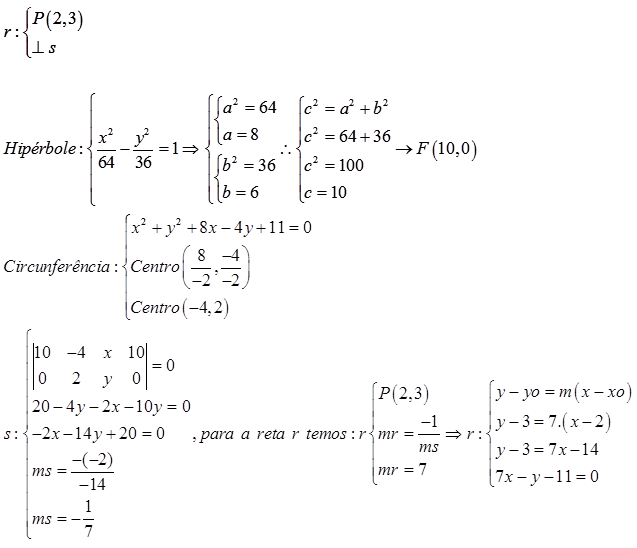
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- Exercícios Resolvidos Equação Geral Da Circunferência
Artigo com exercícios resolvidos equação geral da circunferência 1) Dada a equação x2 + y2 + 2x + 8y + k = 0, obter k para que ela represente: a) uma circunferência; b) um único ponto; c) um conjunto vazio. Resolução 2) Qual das...
- Equação Geral E Reduzida Da Circunferência
artigo sobre circunferência, equação reduzida e geral da circunferência, Posições relativas de uma reta e uma circunferência, propriedades das secantes e tangentes e Posições relativas entre duas circunferências e definição de círculo....
- Questões De Função Exponencial
Faça as seguintes questões de Função exponencial com gabarito e teste seus conhecimentos. Exercícios de Função exponencial 1) As funções y = ax e y = bx com a > 0 e b > 0 e a b têm gráficos que se interceptam em:...
Vestibular
Geometria analítica: estudo da Hipérbole (com questões)
Hipérbole
Definição: Sejam F1 e F2 dois pontos do plano e seja 2c a distância entre eles, hipérbole é o conjunto dos pontos do plano cuja diferença (em módulo) das distâncias à F1 e F2 é a constante 2a (0 < 2a < 2c).
Elementos de uma Hipérbole:
Definição: Sejam F1 e F2 dois pontos do plano e seja 2c a distância entre eles, hipérbole é o conjunto dos pontos do plano cuja diferença (em módulo) das distâncias à F1 e F2 é a constante 2a (0 < 2a < 2c).
Elementos de uma Hipérbole:
F1 e F2 ? são os focos da hipérbole
O ? é o centro da hipérbole
2c ? distância focal
2a ? medida do eixo real ou transverso
2b ? medida do eixo imaginário
c/a ? excentricidade
Existe uma relação entre a, b e c ? c2 = a2 + b2
OBS: Duas hipérboles tais que o eixo focal de cada uma é igual ao eixo não-focal da outra são denominadas hipérboles conjugadas. Como os retângulos de base de duas hipérboles conjugadas são iguais, elas têm o mesmo centro, mesmas assíntotas e os focos a uma mesma distância do centro. 
Equação reduzida da hipérbole de eixo transverso horizontal
Seja P(x, y) um ponto qualquer de uma hipérbole e sejam F1(c,0) e F2(-c,0) os seus focos. Sendo 2.a o valor constante com c > a, como vimos acima, podemos escrever:½ PF1 - PF2 ½ = 2 a
Usando a fórmula da distancia entre dois pontos, poderemos escrever:
Observe que x ? (-c) = x + c.
Quadrando a expressão acima, vem:
Observe que x ? (-c) = x + c.
Quadrando a expressão acima, vem:
Com bastante paciência e aplicando as propriedades corretas, a expressão acima depois de desenvolvida e simplificada, chegará a:b2.x2 - a2.y2 = a2.b2, onde b2 = c2 ? a2 , conforme pode ser verificado na figura acima.
Dividindo agora, ambos os membros por a2b2 vem finalmente:
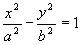
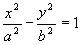
Obs: se o eixo transverso ou eixo real (A1A2) da hipérbole estiver no eixo dos y e o eixo não transverso ou eixo conjugado (B1B2) estiver no eixo dos x, a equação da hipérbole de centro na origem (0,0) passa a ser:
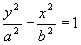
Obs: Em uma hipérbole horizontal teremos x² positivo ( a equação começa com x²), em uma vertical teremos y² positivo ( a equação começa com y²).
Hipérbole equilátera
É aquela em que a = b, ou seja, a medida do semi-eixo real é igual à medida do semi-eixo imaginário.
Cálculo da hipérbole equilátera
Sendo a = b
(eixo real sobre x) x² - y² = a²
(eixo real sobre y) y² - x² = a²
Assímptotas da hipérbole
Assímptotas são retas que contêm as diagonais do retângulo de lados 2a e 2b.
Quando o eixo real é horizontal, o coeficiente angular dessas rectas é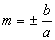 
; quando é vertical, o coeficiente é 
.
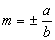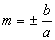; quando é vertical, o coeficiente é 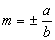.Exemplo: Determine a equação reduzida da hipérbole com eixo real 6, focos F1 (-5 , 0) e
F2 (5, 0).
Solução:
Temos que:
2a = 6 ? a = 3
F1(-5, 0) e F2(5, 0) ? c = 5
Da relação notável, obtemos:
c2 = a2 + b2 ? 52 = 32 + b2 ? b2 =25 ? 9 ? b2 = 16 ? b = 4
Assim, a equação reduzida será dada por:
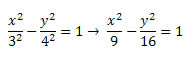
Fonte: www.algosobre.com.br
www.brasilescola.com
www.brasilescola.com
Questões resolvidas sobre hipérbole
1) Determine a distancia focal da hipérbole de equação 25x2 ? 9y2 = 225 .
Dividindo ambos os membros por 225, vem:
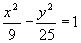
Daí, vem que: a2=9 e b2=25, de onde vem imediatamente: a=3 e b=5.
Portanto, c2 = a2 + b2 = 9 + 25 = 34 e então c = Ö 34.
Logo, a distancia focal da hipérbole sendo igual a 2c , será igual a 2Ö 34.
3 ? Determine as equações das assíntotas da hipérbole do exercício 1.
2) Determine a excentricidade da hipérbole de equação 25x2 - 16y2 ? 400 = 0.
Temos: 25x2 - 16y2 = 400. Observe que a equação da hipérbole não está na forma reduzida. Vamos dividir ambos os membro por 400. Fica então:
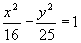
Portanto, a2 = 16 e b2 = 25. Daí, vem: a = 4 e b = 5.
Como c2 = a2 + b2 , vem substituindo e efetuando que c = Ö 41
Portanto a excentricidade
3) (Ufrj) Considere os pontos P (0, 0), P? (1, 1) e P? (2, 6).
a) Determine a equação da parábola que passa por P, P? e P? e tem eixo de simetria paralelo ao eixo Y das ordenadas;
y = 2x£ - x
b) Determine outra parábola que passe pelos pontos P, P? e P?
x = -2/15 y£ + 17/15 y
4) Qual é a medida da distância focal de uma hipérbole cuja medida do eixo imaginário é 24 e a medida do eixo real é 10 ?
(A) 22.
(B) 26.
(C) 28.
(D) 32.
Solução:
Seja a hipérbole de:
eixo real = 10 -> 2*a = 10 => a = 5
eixo imaginário = 24 -> 2*b = 24 => b = 12
temos que: c² = a² + b²
c² - 5² + 12² => c² = 169 => c = 13
a distância focal é dada por:
d(F1,F2) = 2*c => d(F1,F2) = 26.
eixo real = 10 -> 2*a = 10 => a = 5
eixo imaginário = 24 -> 2*b = 24 => b = 12
temos que: c² = a² + b²
c² - 5² + 12² => c² = 169 => c = 13
a distância focal é dada por:
d(F1,F2) = 2*c => d(F1,F2) = 26.
5) Encontre a equação reduzida da hipérbole que possui dois focos com coordenadas F2 (0,10) e eixo imaginário medindo 12.
Solução:
Temos que:
F2(0, 10) ? c = 10
2b = 12 ? b = 6
Utilizando a relação notável, obtemos:
102 = a2 + 62 ? 100 = a2 + 36 ? a2 = 100 ? 36 ? a2 = 64 ? a = 8.
Assim, a equação reduzida da hipérbole será dada por:
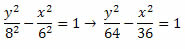
6) Determine a distância focal da hipérbole com equação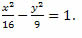 
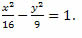
Solução:
Como a equação da hipérbole é do tipo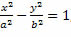 
temos que
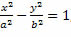temos quea2 = 16 e b2 =9
Da relação notável obtemos
c2 = 16 + 9 ? c2 = 25 ? c = 5
A distância focal é dada por 2c. Assim,
2c = 2*5 =10
Portanto, a distância focal é 10.
Solução:
Como a = b e c² = a² + b², temos que c² = 2a², ou seja, c = Ö 2a.
Logo, e = c/a = Ö 2a/a = Ö 2
8) Encontre a equação da reta que passa pelo ponto P(2,3) e é perpendicular à reta que passa pelo centro da circunferência de equação x² + y² + 8x ? 4y + 11 = 0 e pelo foco de coordenadas positivas da hipérbole de equação
Solução:
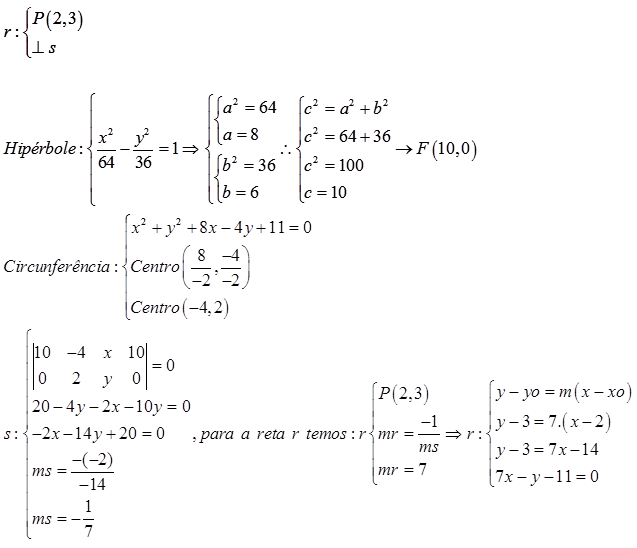
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- Exercícios Resolvidos Equação Geral Da Circunferência
Artigo com exercícios resolvidos equação geral da circunferência 1) Dada a equação x2 + y2 + 2x + 8y + k = 0, obter k para que ela represente: a) uma circunferência; b) um único ponto; c) um conjunto vazio. Resolução 2) Qual das...
- Equação Geral E Reduzida Da Circunferência
artigo sobre circunferência, equação reduzida e geral da circunferência, Posições relativas de uma reta e uma circunferência, propriedades das secantes e tangentes e Posições relativas entre duas circunferências e definição de círculo....
- Questões De Função Exponencial
Faça as seguintes questões de Função exponencial com gabarito e teste seus conhecimentos. Exercícios de Função exponencial 1) As funções y = ax e y = bx com a > 0 e b > 0 e a b têm gráficos que se interceptam em:...