Vestibular
Artigo com exercícios resolvidos equação geral da circunferência
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Geometria Analítica: Estudo Da Hipérbole (com Questões)
Hipérbole Definição: Sejam F1 e F2 dois pontos do plano e seja 2c a distância entre eles, hipérbole é o conjunto dos pontos do plano cuja diferença (em módulo) das distâncias à F1 e F2 é a constante 2a (0 < 2a < 2c). Elementos de uma...
- Polígonos Circunscritos Na Circunferência
Polígonos circunscritos na circunferênciaPolígono circunscrito são polígonos que admite circunferência inscrita. Considerando uma área S como sendo de um polígono circunscrito a uma circunferência de raio r, temos: Onde sabemos que...
- Poligonos Regulares Inscritos Na Circunferencia Questões
Artigo com questões sobre polígonos regulares inscritos na circunferência. 1) Em uma circunferência de raio 8?2 cm encontra-se um quadrado inscrito na mesma. Após fazer a figura, calcule: a) o lado do quadrado L= r?2 L = 8?2 * ?2...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
Vestibular
exercícios resolvidos equação geral da circunferência
Artigo com exercícios resolvidos equação geral da circunferência
1) Dada a equação x2 + y2 + 2x + 8y + k = 0, obter k para que ela represente:

a) uma circunferência;

b) um único ponto;

c) um conjunto vazio.

Resolução

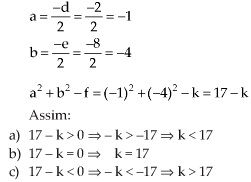

a) uma circunferência;

b) um único ponto;

c) um conjunto vazio.

Resolução

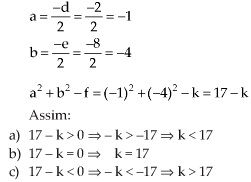
2) Qual das equações abaixo representa uma circunferência?
a) 2x2 + y2 ? 3x + 4y ? 1 = 0
b) x2 + y2 ? 2xy + 4x ? 6y ? 1 = 0
c) x2 + y2 ? 2x ? 2y + 5 = 0
d) x2 ? y2 ? 4x ? 2y ? 1 = 0
e) nda.
Resolução As equações das alternativas a e d não representam uma circunferência, pois os coeficientes de x2 e y2 são diferentes (A
As equações das alternativas a e d não representam uma circunferência, pois os coeficientes de x2 e y2 são diferentes (A  B).
B).
 A equação da alternativa b também não representa uma circunferência, pois o coeficiente de xy não é nulo (C
A equação da alternativa b também não representa uma circunferência, pois o coeficiente de xy não é nulo (C  0).
0).
 A equação da alternativa c, embora pareça representar uma circunferência, não representa, pois, se representasse, o centro da mesma seria C = (1, 1) e a2 + b2 ? f = 12 + 12 ? 5 = ? 3 < 0.
A equação da alternativa c, embora pareça representar uma circunferência, não representa, pois, se representasse, o centro da mesma seria C = (1, 1) e a2 + b2 ? f = 12 + 12 ? 5 = ? 3 < 0.
 Assim, a resposta é alternativa e.
Assim, a resposta é alternativa e. 3) Encontre a equação das circunferências:
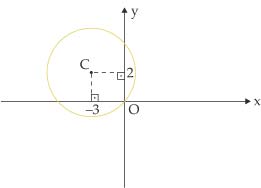
3) Encontre a equação das circunferências: a)
a)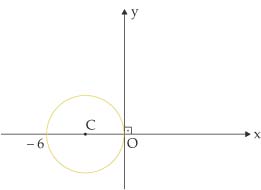
 b)
b)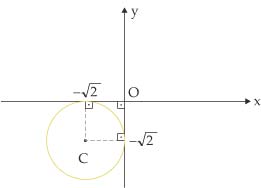

 B).
B).
 0).
0).






c)

d)
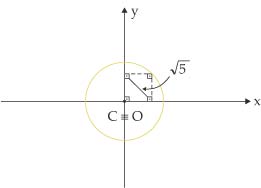


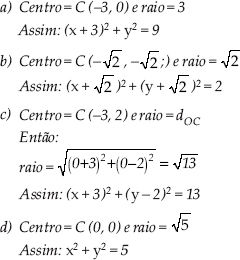
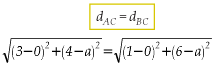

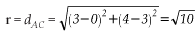




b) x2 + y2 - 2x - 6y = 0
c) x2 + y2 - 4x - 4y = 0
d) x2 + y2 + 4x + 4y = 0
e) n.d.a.


Resolução

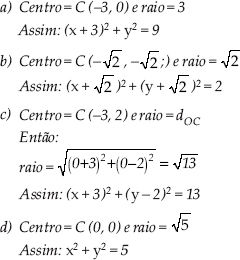
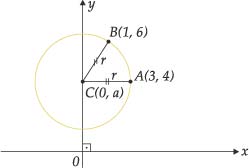
4) Achar a equação reduzida da circunferência com centro no eixo y e que passa pelos pontos A (3, 4) e B (1, 6).
Resolução

Como o centro C pertence ao eixo y, podemos escrever suas coordenadas assim: C = (0, a).


Como A(3,4) e B(1,6) são pontos da circunferência, temos:
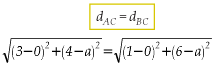

Elevando ao quadrado os dois membros, temos:


9 + 16 ? 8a + a2 = 1 + 36 ? 12a + a2  a = 3
a = 3

 a = 3
a = 3
O centro é o ponto C = (0, 3), e o raio r é:


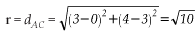

Então, a equação reduzida da circunferência é:


(x ? 0)2 + (y ? 3)2 = 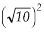
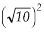

ou seja: x2 + (y ? 3)2 = 10
5) O centro de uma circunferência é determinado pelo ponto médio do segmento PQ, sendo P(4, 6) e Q(2, 10). Considerando que o raio dessa circunferência é 7, determine sua equação.

6) (FEI-SP) Determine a equação da circunferência com centro no ponto C(2, 1) e que passa pelo ponto A(1, 1).
Resolução

7) Ache a equação geral da circunferência que passa pela origem e tem centro C(- 1,- 4).
Resolução:
C(-1,-4) passando pela origem(0,0)
Com essa informação vc consegue calcular o raio R:
R=?[(-1-0)²+(-4-0)²]= ?17
(x+1)²+(y+4)² =17
x²+2x+1+y²+8y+16-17=0
x²+y²+2x+8y=0 <= Equação geral
Com essa informação vc consegue calcular o raio R:
R=?[(-1-0)²+(-4-0)²]= ?17
(x+1)²+(y+4)² =17
x²+2x+1+y²+8y+16-17=0
x²+y²+2x+8y=0 <= Equação geral
8) Ache a equação geral da circunferência que passa (2 , -3) , (5 , 0) e (-1 , -4)
Resolução:
A(2 , -3) , B(5 , 0) e C(-1 , -4)
A circunferência passa por esses 3 pontos, certo?
Toda circunferência tem um centro, certo?
Ora, a distância entre cada ponto acima e o centro é a mesma(que é o raio da circunferência).
Então, devo aplicar distância entre 2 pontos e igualar as equações.
Seja P(a,b) o CENTRO da circunferência.A distância entre P e A é a mesma entre P e B, afinal se trata do raio.
Assim:
Dp,a=?[(Xa-Xp)²+(Ya-Yp)²]
Dp,b=?[(Xb-Xp)²+(Yb-Yp)²]
Dp,a=Dp,b
(2-a)²+(-3-b)²=(5-a)²+(0-b)²
4-4a+a²+9+6b+b²= 25-10a+a²+b²
-4a+6b+13 = 25-10a
6a+6b = 12
a+b=2 <= (Equação 1)
Agora faça:
Dp,c=Dp,b
Dp,c=?[(Xc-Xp)²+(Yc-Yp)²]
Dp,b=?[(Xb-Xp)²+(Yb-Yp)²]
(-1-a)²+(-4-b)²=(5-a)²+(0-b)²
1+2a+a²+16-8b+b²=25-10a+a²+b²
2a-8b+17=25-10a
12a-8b=8
3a-2b=2 <= (Equação 2)
Temos duas equações e duas incógnitas:
a+b=2
3a-2b=2
Resolva do jeito que achar melhor:
resp:
a=-2
b=+4
Assim, o centro da circunferência que passa por esses pontos é dado por: P(-2,4)
Raio=?[(Xa-Xp)²+(Ya-Yp)²]
=?[(2+2)²+(-3-4)²]=?(16+49)=?65
A circunferência passa por esses 3 pontos, certo?
Toda circunferência tem um centro, certo?
Ora, a distância entre cada ponto acima e o centro é a mesma(que é o raio da circunferência).
Então, devo aplicar distância entre 2 pontos e igualar as equações.
Seja P(a,b) o CENTRO da circunferência.A distância entre P e A é a mesma entre P e B, afinal se trata do raio.
Assim:
Dp,a=?[(Xa-Xp)²+(Ya-Yp)²]
Dp,b=?[(Xb-Xp)²+(Yb-Yp)²]
Dp,a=Dp,b
(2-a)²+(-3-b)²=(5-a)²+(0-b)²
4-4a+a²+9+6b+b²= 25-10a+a²+b²
-4a+6b+13 = 25-10a
6a+6b = 12
a+b=2 <= (Equação 1)
Agora faça:
Dp,c=Dp,b
Dp,c=?[(Xc-Xp)²+(Yc-Yp)²]
Dp,b=?[(Xb-Xp)²+(Yb-Yp)²]
(-1-a)²+(-4-b)²=(5-a)²+(0-b)²
1+2a+a²+16-8b+b²=25-10a+a²+b²
2a-8b+17=25-10a
12a-8b=8
3a-2b=2 <= (Equação 2)
Temos duas equações e duas incógnitas:
a+b=2
3a-2b=2
Resolva do jeito que achar melhor:
resp:
a=-2
b=+4
Assim, o centro da circunferência que passa por esses pontos é dado por: P(-2,4)
Raio=?[(Xa-Xp)²+(Ya-Yp)²]
=?[(2+2)²+(-3-4)²]=?(16+49)=?65
Equação reduzida:
(x+2)²+(y-4)²=65
Equação Geral:
x²+y²+4x-8y-45=0
(x+2)²+(y-4)²=65
Equação Geral:
x²+y²+4x-8y-45=0
Agora pratique:
exercícios propostos equação da circunferência
1) (UEMT) Dada a circunferência C da equação (x - 1)² + y²= 1 e considerando o ponto P(2, 1), então as retas tangentes a C passando por P:
a) Têm equações y = 1 e x = 2.
b) não existem pois P é interno a C.
c) são ambas paralelas à reta y =1
d) Têm equações y = 1 (e só uma porque P está em C).
c) Têm equações x = 1 e y = 2.
a) Têm equações y = 1 e x = 2.
b) não existem pois P é interno a C.
c) são ambas paralelas à reta y =1
d) Têm equações y = 1 (e só uma porque P está em C).
c) Têm equações x = 1 e y = 2.
2) (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x² + y² - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
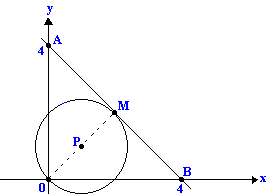
3) Se M é o ponto médio do segmento AB e P é o ponto médio do segmento OM, determinar a equação da circunferência de centro P e raio OP.

4) A equação da circunferência que tangencia as retas x + y = 0 e x + y = 8 e que passa pelo ponto (0; 0) é:
a) 2 . x2 + 2y2 - 4x - 4y = 0b) x2 + y2 - 2x - 6y = 0
c) x2 + y2 - 4x - 4y = 0
d) x2 + y2 + 4x + 4y = 0
e) n.d.a.
gabarito:
1. A 2. D 3. (x - 1)2 + (y-1)2 = 2 4. C
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Geometria Analítica: Estudo Da Hipérbole (com Questões)
Hipérbole Definição: Sejam F1 e F2 dois pontos do plano e seja 2c a distância entre eles, hipérbole é o conjunto dos pontos do plano cuja diferença (em módulo) das distâncias à F1 e F2 é a constante 2a (0 < 2a < 2c). Elementos de uma...
- Polígonos Circunscritos Na Circunferência
Polígonos circunscritos na circunferênciaPolígono circunscrito são polígonos que admite circunferência inscrita. Considerando uma área S como sendo de um polígono circunscrito a uma circunferência de raio r, temos: Onde sabemos que...
- Poligonos Regulares Inscritos Na Circunferencia Questões
Artigo com questões sobre polígonos regulares inscritos na circunferência. 1) Em uma circunferência de raio 8?2 cm encontra-se um quadrado inscrito na mesma. Após fazer a figura, calcule: a) o lado do quadrado L= r?2 L = 8?2 * ?2...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
