Vestibular
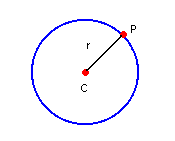
A circunferência é o lugar geométrico de todos os pontos de um plano que estão localizados a uma mesma distância r de um ponto fixo denominado o centro da circunferência.
A circunferência possui características não comumente encontradas em outras figuras planas, como o fato de ser a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente. É também a única figura que é simétrica em relação a um número infinito de eixos de simetria. A circunferência é importante em praticamente todas as áreas do conhecimento como nas Engenharias, Matemática, Física, Química, Biologia, Arquitetura, Astronomia, Artes e também é muito utilizado na indústria e bastante utilizada nas residências das pessoas.
Desenvolvendo a equação reduzida, obtemos a equação geral da circunferência:
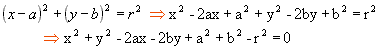
Como exemplo, vamos determinar a equação geral da circunferência de centro C(2, -3) e raio r = 4.
A equação reduzida da circunferência é:
( x - 2 )2 +( y + 3 )2 = 16
Desenvolvendo os quadrados dos binômios, temos:
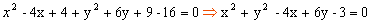
Posições relativas de uma reta e uma circunferência
Tangente ? é a reta que tem um único ponto comum à circunferência, este ponto é conhecido como ponto de tangência ou ponto de contato.
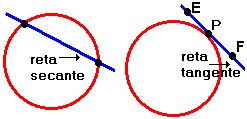
Secante ? é a reta que intercepta a circunferência em dois pontos distintos, se essa reta intercepta a circunferência em dois pontos quaisquer, podemos dizer também que é a reta que contem uma corda.
Propriedades das secantes e tangentes
Internas D < r1 ? r2


Possuem dois pontos em comum
Secante: possuem dois pontos em comum.
r1 ? r2 < D < r1 + r2
Circunferências concêntricas
São circunferências que possuem o mesmo centro, não existindo distância entre eles.
D = 0
Círculo: (ou disco) é o conjunto de todos os pontos de um plano cuja distância a um ponto fixo O é menor ou igual que uma distância r dada. Quando a distância é nula, o círculo se reduz a um ponto. O círculo é a reunião da circunferência com o conjunto de pontos localizados dentro da mesma. No gráfico acima, a circunferência é a linha de cor verde-escuro que envolve a região verde, enquanto o círculo é toda a região pintada de verde reunida com a circunferência.
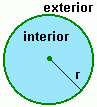
Pontos exteriores: Os pontos exteriores a um círculo são os pontos localizados fora do círculo.
Raio, corda e diâmetro
Raio: Raio de uma circunferência (ou de um círculo) é um segmento de reta com uma extremidade no centro da circunferência e a outra extremidade num ponto qualquer da circunferência. Na figura, os segmentos de reta OA, OB e OC são raios.
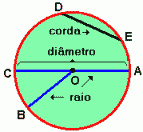
Corda: Corda de uma circunferência é um segmento de reta cujas extremidades pertencem à circunferência. Na figura, os segmentos de reta AC e DE são cordas.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência. Na figura, o segmento de reta AC é um diâmetro.
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...
- Polígonos Circunscritos Na Circunferência
Polígonos circunscritos na circunferênciaPolígono circunscrito são polígonos que admite circunferência inscrita. Considerando uma área S como sendo de um polígono circunscrito a uma circunferência de raio r, temos: Onde sabemos que...
- Poligonos Regulares Inscritos Na Circunferencia Questões
Artigo com questões sobre polígonos regulares inscritos na circunferência. 1) Em uma circunferência de raio 8?2 cm encontra-se um quadrado inscrito na mesma. Após fazer a figura, calcule: a) o lado do quadrado L= r?2 L = 8?2 * ?2...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
Vestibular
Equação geral e reduzida da circunferência
artigo sobre circunferência, equação reduzida e geral da circunferência, Posições relativas de uma reta e uma circunferência, propriedades das secantes e tangentes e Posições relativas entre duas circunferências e definição de círculo.
A circunferência é o lugar geométrico de todos os pontos de um plano que estão localizados a uma mesma distância r de um ponto fixo denominado o centro da circunferência.

A circunferência possui características não comumente encontradas em outras figuras planas, como o fato de ser a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente. É também a única figura que é simétrica em relação a um número infinito de eixos de simetria. A circunferência é importante em praticamente todas as áreas do conhecimento como nas Engenharias, Matemática, Física, Química, Biologia, Arquitetura, Astronomia, Artes e também é muito utilizado na indústria e bastante utilizada nas residências das pessoas.
Equação reduzida da circunferência
Uma circunferência é determinada quando conhecemos a posição do seu centro e o valor do seu raio. Imaginando no plano cartesiano uma circunferência de centro no ponto C = (a, b) e com raio R, vamos representar por P = (x, y) um ponto qualquer que pertence a essa circunferência. Que propriedade tem o ponto P?
Se P pertence à circunferência, sua distância até o centro é igual ao raio.
Como a distância do ponto C = (a, b) ao ponto P = (x, y) é igual a R, usando a fórmula da distância entre dois pontos temos:
(x - a)2 + (y - b)2 = R
Elevando ao quadrado os dois membros, a expressão obtida é a equação da circunferência de centro (a, b) e raio R.


Uma circunferência é determinada quando conhecemos a posição do seu centro e o valor do seu raio. Imaginando no plano cartesiano uma circunferência de centro no ponto C = (a, b) e com raio R, vamos representar por P = (x, y) um ponto qualquer que pertence a essa circunferência. Que propriedade tem o ponto P?
Se P pertence à circunferência, sua distância até o centro é igual ao raio.
Como a distância do ponto C = (a, b) ao ponto P = (x, y) é igual a R, usando a fórmula da distância entre dois pontos temos:
(x - a)2 + (y - b)2 = R
Elevando ao quadrado os dois membros, a expressão obtida é a equação da circunferência de centro (a, b) e raio R.


Portanto, (x - a)² + (y - b)² = r² é a equação reduzida da circunferência e permite determinar os elementos essenciais para a construção da circunferência: as coordenadas do centro e o raio.
Observação: Quando o centro da circunferência estiver na origem (C(0,0)), a equação da circunferência seráx² + y² = r² .
Exemplo:
Seja uma circunferência cuja equação é:
(x - 2) ² + (y - 3)² = 100
Verificar se a circunferência passa pela origem ,quais as coordenadas do centro e quanto vale o raio:
Pela expressão temos que: R = 10 e C(2,3)
Fazendo x=0 e y=0, temos que: (-2) ² + (-3) ² = 13
Como 13 é diferente de 100, logo a circunferência não passa pela origem.
Equação geral
Desenvolvendo a equação reduzida, obtemos a equação geral da circunferência:
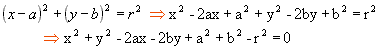
Como exemplo, vamos determinar a equação geral da circunferência de centro C(2, -3) e raio r = 4.
A equação reduzida da circunferência é:
( x - 2 )2 +( y + 3 )2 = 16
Desenvolvendo os quadrados dos binômios, temos:
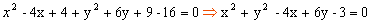
Aplicação
Determine as equações da circunferência de centro (1, 5) e raio 2.
Solução:
Sendo a = 1, b = 5 e r = 2, então, temos:
Sendo a = 2, b = 4 e r = 3, então, temos:
(x ? a)2 + (y ? b)2 = r2 (x ? 1)2 + (y ? 5)2 = 22
(x ? 1)2 + (y ? 5)2 = 4 (equação reduzida)
(x ? 1)2 + (y ? 5)2 = 4
x2 ? 2x + 1 + y2 ? 10y + 25 ? 4 = 0
x2 + y2 ? 2x ? 10y + 22 = 0 (equação geral)
Tangente ? é a reta que tem um único ponto comum à circunferência, este ponto é conhecido como ponto de tangência ou ponto de contato.

Secante ? é a reta que intercepta a circunferência em dois pontos distintos, se essa reta intercepta a circunferência em dois pontos quaisquer, podemos dizer também que é a reta que contem uma corda.
Propriedades das secantes e tangentes
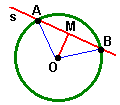
- Se uma reta s, secante a uma circunferência de centro O, intercepta a circunferência em dois pontos distintos A e B e se M é o ponto médio da corda AB, então o segmento de reta OM é perpendicular à reta secante s.
- Se uma reta s, secante a uma circunferência de centro O, intercepta a circunferência em dois pontos distintos A e B, a perpendicular à reta s que passa pelo centro O da circunferência, passa também pelo ponto médio da corda AB.
- Seja OP um raio de uma circunferência, onde O é o centro e P um ponto da circunferência. Toda reta perpendicular ao raio OP é tangente à circunferência no ponto de tangência P.
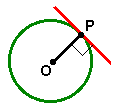
- Toda reta tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
Posições relativas entre duas circunferências
Não possuem pontos em comum
Externas D > r1 + r2

Não possuem pontos em comum
Externas D > r1 + r2

Internas D < r1 ? r2

Possuem um ponto em comum
Tangentes: as circunferências possuem um ponto em comum.
Tangentes internas D = r1 ? r2
Tangentes: as circunferências possuem um ponto em comum.
Tangentes internas D = r1 ? r2

Tangentes externas
D = r1 + r2
D = r1 + r2

Possuem dois pontos em comum
Secante: possuem dois pontos em comum.
r1 ? r2 < D < r1 + r2

Circunferências concêntricas
São circunferências que possuem o mesmo centro, não existindo distância entre eles.
D = 0

Círculo: (ou disco) é o conjunto de todos os pontos de um plano cuja distância a um ponto fixo O é menor ou igual que uma distância r dada. Quando a distância é nula, o círculo se reduz a um ponto. O círculo é a reunião da circunferência com o conjunto de pontos localizados dentro da mesma. No gráfico acima, a circunferência é a linha de cor verde-escuro que envolve a região verde, enquanto o círculo é toda a região pintada de verde reunida com a circunferência.
Pontos interiores de um círculo e exteriores a um círculo
Pontos interiores: Os pontos interiores de um círculo são os pontos do círculo que não estão na circunferência.
Pontos exteriores: Os pontos exteriores a um círculo são os pontos localizados fora do círculo.

Pontos exteriores: Os pontos exteriores a um círculo são os pontos localizados fora do círculo.
Raio: Raio de uma circunferência (ou de um círculo) é um segmento de reta com uma extremidade no centro da circunferência e a outra extremidade num ponto qualquer da circunferência. Na figura, os segmentos de reta OA, OB e OC são raios.

Corda: Corda de uma circunferência é um segmento de reta cujas extremidades pertencem à circunferência. Na figura, os segmentos de reta AC e DE são cordas.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência. Na figura, o segmento de reta AC é um diâmetro.
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...
- Polígonos Circunscritos Na Circunferência
Polígonos circunscritos na circunferênciaPolígono circunscrito são polígonos que admite circunferência inscrita. Considerando uma área S como sendo de um polígono circunscrito a uma circunferência de raio r, temos: Onde sabemos que...
- Poligonos Regulares Inscritos Na Circunferencia Questões
Artigo com questões sobre polígonos regulares inscritos na circunferência. 1) Em uma circunferência de raio 8?2 cm encontra-se um quadrado inscrito na mesma. Após fazer a figura, calcule: a) o lado do quadrado L= r?2 L = 8?2 * ?2...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
