Vestibular
Artigo sobre área do Trapézio e questões de vestibular para uma melhor fixação do conteúdo.
O trapézio pode ser definido como um quadrilátero notável, pois a soma dos seus ângulos internos é igual a 360º. É Formado por segmentos de retas que recebem o nome de lado. O encontro dos lados recebe o nome de vértices. Por ser uma figura fechada possui superfície que também é chamada de área.
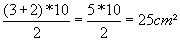
Solução:
Dados
A = 45 cm2
B = 11 cm
b = 7 cm
Substituindo os dados na fórmula da área, teremos: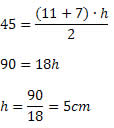
4) Um trapézio isósceles com bases medindo 12 cm e 16 cm está inscrito em uma circunferência de raio 10 cm. Calcular a área do trapézio, se o centro da circunferência não está no interior do trapézio.
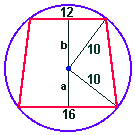
Na figura acima a altura h do trapézio é dada por h=b-a, onde:
a² = 10² - 8² = 36
A = (1/2)(B+b)h = (1/2)(16+12).2 = 28 cm².
5) Calcular a área do trapézio isósceles traçado ao lado se todos os seus lados são tangentes à circunferência e as medidas são dadas em cm.
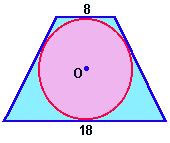
Vamos construir um triângulo isósceles com o prolongamento dos lados não paralelos do trapézio, de acordo com a figura abaixo.
Tomaremos h=AE e r o raio da circunferência inscrita no trapézio.
BC=18 e DF=8, logo GC=9 e EF=4.
Como o trapézio BCFD é isósceles, o triângulo ABC é isósceles.
O triângulo AGC é retângulo com ângulo reto em G.
O triângulo AEF é retângulo com ângulo reto em E e por semelhança de triângulos, temos que: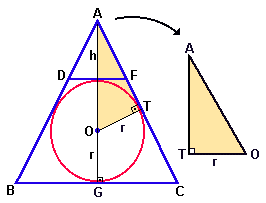
O triângulo ATO tem um ângulo reto em T, porque T é ponto de tangência. Este triângulo ATO também é semelhante ao triângulo AGC, logo:AT/TO = AG/GC
m(AT)/r = (h+2r)/9 (*)
Acontece que AT = R[h2+2hr] = R[16r2/25 + 2r(8r)/5] = 12r / 5
Substituindo este valor em (*), obtemos:
6) (UFPE) A área do trapézio (figura abaixo) é igual a 
A) 86
B) 96
C) 106
D) 116
E) 126
Resposta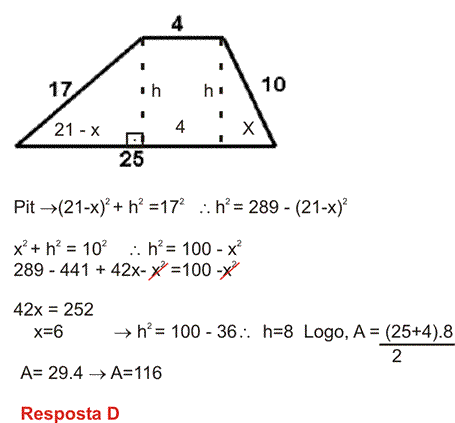
8) O trapézio ABCD foi divido em dois retângulos AEGF e FGCD, um triângulo GHC e um trapézio EBHG. As áreas dos dois retângulos e do triângulo, em cm2, estão indicadas na figura. Qual é a área do trapézio EBHG?
- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- Retângulo Questões Vestibular
O retângulo é um quadrilátero, pois possui 4 lados que podem ou não ser iguais. Quando os lados forem diferentes ela continua recebendo o nome de retângulo, agora quando os 4 lados forem iguais o retângulo poderá ser chamado de quadrado. O cálculo...
- Áreas De Figuras Planas Fórmulas E Exemplos
Áreas de figuras planas fórmulas e exemplos Área do Retângulo e do Triângulo No retângulo a seguir foi traçada uma de suas diagonais, dividindo a figura em duas partes iguais. Note que a área total do retângulo é dada pela expressão A...
- Relações Métricas No Triângulo Retângulo - Geometria
Artigo sobre relações métricas no triângulo retângulo e aplicações do Teorema de Pitágoras geometria. Triângulo retângulo é todo triângulo que tem um ângulo reto. Todo triângulo retângulo é composto por dois catetos e uma hipotenusa....
Vestibular
Trapézio questões vestibular
Artigo sobre área do Trapézio e questões de vestibular para uma melhor fixação do conteúdo.
O trapézio pode ser definido como um quadrilátero notável, pois a soma dos seus ângulos internos é igual a 360º. É Formado por segmentos de retas que recebem o nome de lado. O encontro dos lados recebe o nome de vértices. Por ser uma figura fechada possui superfície que também é chamada de área.
O trapézio possui dois lados paralelos correspondentes às suas bases, uma maior e outra menor que nunca possuirão ponto em comum. Observe:
Dizemos que os lados AB e DC são paralelos e constituem as duas bases do trapézio, considerando nesse caso que:
AB: menor base.
DC: maior base.
AB: menor base.
DC: maior base.
Vamos conhecer agora os tipos de trapézios existentes de acordo com a Geometria plana: Trapézio retângulo, Trapézio isósceles e Trapézio escaleno.
Trapézio retângulo: possui dois ângulos retos (90º).
Trapézio isósceles: os lados não paralelos possuem medidas iguais.
Trapézio escaleno: os lados possuem medidas de tamanhos diferentes.
Trapézio isósceles: os lados não paralelos possuem medidas iguais.
Trapézio escaleno: os lados possuem medidas de tamanhos diferentes.
Consideremos um trapézio qualquer, traçando uma de suas diagonais, podemos dividi-lo em duas regiões triangulares de altura h e bases B (b1) e b (b2).
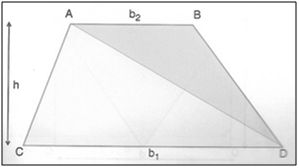
Temos que a área de uma região triangular é dada por A = (b x h) / 2, então a área do trapézio será:
Exemplo: Calcule a área do trapézio abaixo:
O trapézio tem área igual a 29 unidades de área.
Exercícios sobre área do trapézio
1) Determine a medida da base maior de um trapézio com 150 cm² de área, 10 cm de altura e base menor medindo 12 cm.
Dados do problema:
A = 150 cm² h = 10 cm b = 12 cm B = x
Solução:
150 = (B + 12) . 10/2
300 = (B + 12) . 10
300/10 = B + 12
B + 12 = 30
B = 30 ? 12
B = 18 cm
Temos, B = 18 cm
2) Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio?
Solução:
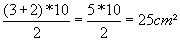
3) Determine a altura de um trapézio de 45 cm2 de área, base maior medindo 11 cm e base menor com 7 cm de comprimento.
Solução:
Dados
A = 45 cm2
B = 11 cm
b = 7 cm
Substituindo os dados na fórmula da área, teremos:
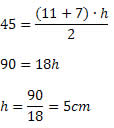
4) Um trapézio isósceles com bases medindo 12 cm e 16 cm está inscrito em uma circunferência de raio 10 cm. Calcular a área do trapézio, se o centro da circunferência não está no interior do trapézio.
Solução:
Na figura acima a altura h do trapézio é dada por h=b-a, onde:
a² = 10² - 8² = 36
a = 6
b² = 10² - 6² = 64
b=8
h = 8 - 6 = 2 cm
A = (1/2)(B+b)h = (1/2)(16+12).2 = 28 cm².
5) Calcular a área do trapézio isósceles traçado ao lado se todos os seus lados são tangentes à circunferência e as medidas são dadas em cm.
Solução:
Vamos construir um triângulo isósceles com o prolongamento dos lados não paralelos do trapézio, de acordo com a figura abaixo.
Tomaremos h=AE e r o raio da circunferência inscrita no trapézio.
BC=18 e DF=8, logo GC=9 e EF=4.
Como o trapézio BCFD é isósceles, o triângulo ABC é isósceles.
O triângulo AGC é retângulo com ângulo reto em G.
O triângulo AEF é retângulo com ângulo reto em E e por semelhança de triângulos, temos que:
- AE / EF = AG / GC implica que h / 4 = (h + 2r) / 9
h = 8r / 5
O triângulo ATO tem um ângulo reto em T, porque T é ponto de tangência. Este triângulo ATO também é semelhante ao triângulo AGC, logo:AT/TO = AG/GCm(AT)/r = (h+2r)/9 (*)
Acontece que AT = R[h2+2hr] = R[16r2/25 + 2r(8r)/5] = 12r / 5
Substituindo este valor em (*), obtemos:
12r / 5r = (h+2r) / 9
12/5 = (8r/5 + 2r) / 9
r = 6
Atrapézio = (Bmaior + Bmenor).h/2
Atrapézio = (18+8).2.6/2 = 78
6) (UFPE) A área do trapézio (figura abaixo) é igual a
A) 86
B) 96
C) 106
D) 116
E) 126
Resposta
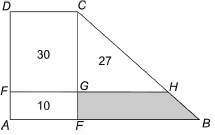
8) O trapézio ABCD foi divido em dois retângulos AEGF e FGCD, um triângulo GHC e um trapézio EBHG. As áreas dos dois retângulos e do triângulo, em cm2, estão indicadas na figura. Qual é a área do trapézio EBHG?
|
- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- Retângulo Questões Vestibular
O retângulo é um quadrilátero, pois possui 4 lados que podem ou não ser iguais. Quando os lados forem diferentes ela continua recebendo o nome de retângulo, agora quando os 4 lados forem iguais o retângulo poderá ser chamado de quadrado. O cálculo...
- Áreas De Figuras Planas Fórmulas E Exemplos
Áreas de figuras planas fórmulas e exemplos Área do Retângulo e do Triângulo No retângulo a seguir foi traçada uma de suas diagonais, dividindo a figura em duas partes iguais. Note que a área total do retângulo é dada pela expressão A...
- Relações Métricas No Triângulo Retângulo - Geometria
Artigo sobre relações métricas no triângulo retângulo e aplicações do Teorema de Pitágoras geometria. Triângulo retângulo é todo triângulo que tem um ângulo reto. Todo triângulo retângulo é composto por dois catetos e uma hipotenusa....