Vestibular
Áreas de figuras planas fórmulas e exemplos
- área Do Quadrado Questões Vestibular
Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S= 36 cm Quando dispomos da medida das diagonais do quadrado,...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...
- Retângulo Questões Vestibular
O retângulo é um quadrilátero, pois possui 4 lados que podem ou não ser iguais. Quando os lados forem diferentes ela continua recebendo o nome de retângulo, agora quando os 4 lados forem iguais o retângulo poderá ser chamado de quadrado. O cálculo...
- área Do Quadrado Questões Vestibular
Artigo sobre área do quadrado com questões de fixação. Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S=...
- área Do Losango Questões Vestibular
Artigo sobre como calcular a área de um losango com exercícios para melhor fixação do conteúdo. Losango é uma figura plana conhecida como quadrilátero, possuindo assim duas diagonais e quatro lados congruentes. O seu diferencial com relação às...
Vestibular
Áreas de figuras planas fórmulas e exemplos
Áreas de figuras planas fórmulas e exemplos
Área do Retângulo e do Triângulo
Exemplo: A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
Do enunciado temos:

Utilizando a fórmula:

Atribuindo 5 à variável h e 25 à variável b temos:

Utilizando a fórmula:

A área deste terreno é de 125 m².
Área do Triângulo Equilátero


Área do Trapézio
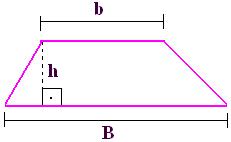
Um trapézio é formado por uma base maior (B), por uma base menor (b) e por uma altura (h).

Solução: a figura é um trapézio de base maior medindo 30 cm, base menor medindo 18 cm e altura com 10 cm de comprimento. Aplicando a fórmula da área, obtemos:

Área do quadrado
exemplo: A área de um quadrado é igual a 196 cm². Qual a medida do lado deste quadrado?
Temos que S é igual a 196.

Utilizando a fórmula temos:


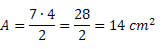
exemplo 2: Calcule a área de um losango de 5 cm de lado e diagonal menor medindo 6 cm.
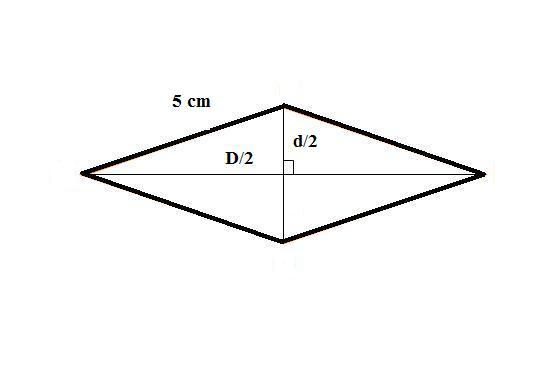
Solução: para o cálculo da área precisamos conhecer as medidas das duas diagonais, mas o problema nos forneceu apenas a da diagonal menor. Dessa forma, precisamos determinar a medida da diagonal maior.
Utilizando o teorema de Pitágoras, temos que:
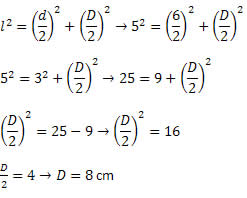
Conhecendo as medidas das duas diagonais, basta utilizar a fórmula da área. Assim,
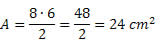
Solução: De acordo com o enunciado do problema, sabemos que b = 15 cm e h = 12 cm.
Assim, podemos aplicar a fórmula da área do paralelogramo.
A = base x altura
A = 15 x 12
A = 180 cm2.
Não se esqueça que as unidades de medida de área sempre estão elevadas ao quadrado: m2, cm2, km2, etc.
Exemplo 2. Determine a área da figura abaixo: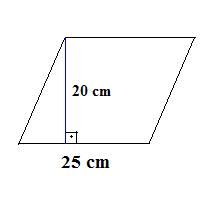
A = base x altura
A = 25 x 20
A = 500 cm2
Portanto, o paralelogramo da figura apresenta uma área de 500 cm2.Cálculo da Área do Círculo



Do enunciado, temos que o valor do raio r é:




Exemplo:
Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Aplicando a fórmula em graus temos:

A área do setor circular é de 37,6992 cm².
Cálculo da Área de Coroas Circulares
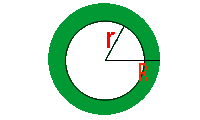

Se a largura é de 5 cm, significa que r = 20 - 5 = 15, substituindo na fórmula temos:

A área da coroa circular é de 549,78 cm².
Questões
1) Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a área deste triângulo?
Perímetro:
6*3 = 18cm
Área: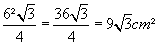
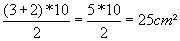
Resolução:
Se observarmos bem, vemos que a parte de baixo da figura roxa se encaixa na parte branca de cima da figura. Logo, temos um retângulo
4*2 = 8
Solução: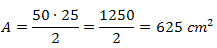
No retângulo a seguir foi traçada uma de suas diagonais, dividindo a figura em duas partes iguais.

Note que a área total do retângulo é dada pela expressão A = b x h, considerando que a diagonal dividiu o retângulo em duas partes iguais formando dois triângulos, a área de cada triângulo será igual à metade da área total do retângulo, constituindo na seguinte expressão matemática:


Note que a área total do retângulo é dada pela expressão A = b x h, considerando que a diagonal dividiu o retângulo em duas partes iguais formando dois triângulos, a área de cada triângulo será igual à metade da área total do retângulo, constituindo na seguinte expressão matemática:

Exemplo: A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
Do enunciado temos:
Utilizando a fórmula:
A área deste triângulo é 12,25 cm².
Exemplo 2: Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Exemplo 2: Um terreno mede 5 metros de largura por 25 metros de comprimento. Qual é a área deste terreno?
Atribuindo 5 à variável h e 25 à variável b temos:
Utilizando a fórmula:
A área deste terreno é de 125 m².
Área do Triângulo Equilátero
Observe o triângulo de vértices A, B e C com lados medindo a e altura h.

Observe que o triângulo equilátero possui os três ângulos internos iguais, assim como os seus três lados, podemos utilizar a seguinte fórmula:


Exemplo:
Determine a medida da área de uma região triangular equilátera, com lados medindo 12 metros de comprimento.

A região triangular possui área medindo 36?3 metros.

DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...
Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de
DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR
Área do Trapézio
Um trapézio é formado por uma base maior (B), por uma base menor (b) e por uma altura (h).
o cálculo de sua área é dado pela seguinte fórmula:
A = h (B + b)
2
h = altura
B = base maior do trapézio
b = base menor do trapézio
A = h (B + b)
2
h = altura
B = base maior do trapézio
b = base menor do trapézio
Exemplo: Determine a área da figura abaixo:

Solução: a figura é um trapézio de base maior medindo 30 cm, base menor medindo 18 cm e altura com 10 cm de comprimento. Aplicando a fórmula da área, obtemos:

Área do quadrado
Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado. Exemplo: O lado de um quadrado mede 8 cm.
A = L x L
A= 8×8
A= 64 cm
A= 8×8
A= 64 cm
Temos que S é igual a 196.
Utilizando a fórmula temos:
Área do Losango
A área do losango é a diagonal menor multiplicado pela diagonal maior dividido tudo por dois.

Exemplo: Calcule a área de um losango de diagonais medindo 7 cm e 4 cm.
Solução: foram dados D = 7 cm e d = 4 cm. Dessa forma, basta substituir os valores na fórmula da área. Assim,
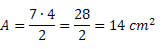
Utilizando o teorema de Pitágoras, temos que:
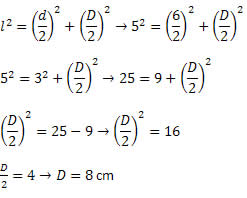
Conhecendo as medidas das duas diagonais, basta utilizar a fórmula da área. Assim,
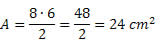
Área do Paralelogramo
A fórmula usada para calcular a área de um paralelogramo é A = b x h (b: base e h: altura), sendo que a altura é perpendicular a base.
Exemplo 1: Calcule a área de um paralelogramo cuja base mede 15 cm e a altura 12 cm.
Assim, podemos aplicar a fórmula da área do paralelogramo.
A = base x altura
A = 15 x 12
A = 180 cm2.
Não se esqueça que as unidades de medida de área sempre estão elevadas ao quadrado: m2, cm2, km2, etc.
Exemplo 2. Determine a área da figura abaixo:
Solução: A figura acima é um paralelogramo (veja os lados opostos paralelos) cuja base mede 25 cm e a altura, 20 cm. Observe que a altura forma um ângulo de 90o (ângulo reto) com a base. Como sabemos as medidas da altura e da base, basta utilizar a fórmula da área. Assim, teremos:
A = base x altura
A = 25 x 20
A = 500 cm2
Portanto, o paralelogramo da figura apresenta uma área de 500 cm2.

A divisão do perímetro de uma circunferência, pelo seu diâmetro resultará sempre no mesmo valor, qualquer que seja circunferência. Este valor irracional constante é representado pela letra grega minúscula pi, grafada como:
Por ser um número irracional, o número pi possui infinitas casas decimais. Para cálculos corriqueiros, podemos utilizar o valor 3,14159265. Para cálculos com menos precisão, podemos utilizar 3,1416, ou até mesmo 3,14.
O perímetro de uma circunferência é obtido através da fórmula:
O cálculo da área do círculo é realizado segundo a fórmula abaixo:
Onde r representa o raio do círculo.
Exemplo: Um círculo tem raio de 8,52 mm. Quantos milímetros quadrados ele possui de superfície?
Do enunciado, temos que o valor do raio r é:
Ao substituirmos valor de r na fórmula teremos:
A superfície do círculo é de 228,05 mm².
Cálculo da Área de Setores Circulares

O cálculo da área de um setor circular pode ser realizado calculando-se a área total do círculo e depois se montando uma regra de três, onde a área total do círculo estará para 360°, assim como a área do setor estará para o número de graus do setor.
Sendo S a área total do círculo, S? a área do setor circular e ? o seu número de graus, temos:
Em radianos temos:
A partir destas sentenças podemos chegar a esta fórmula em graus:
E a esta outra em radianos:
Onde r representa o raio do círculo referente ao setor e ? é o ângulo também referente ao setor.
Exemplo:
Qual é a área de um setor circular com ângulo de 30° e raio de 12 cm?
Aplicando a fórmula em graus temos:
A área do setor circular é de 37,6992 cm².
Cálculo da Área de Coroas Circulares

O cálculo da área de uma coroa circular pode ser realizado calculando-se a área total do círculo e subtraindo-se desta, a área do círculo inscrito. Podemos também utilizar a seguinte fórmula:
Onde R representa o raio do círculo e r representa o raio do círculo inscrito.
Exemplo: Qual é a área de uma coroa circular com raio de 20 cm e largura de 5 cm?
Se a largura é de 5 cm, significa que r = 20 - 5 = 15, substituindo na fórmula temos:
A área da coroa circular é de 549,78 cm².
Questões
1) Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a área deste triângulo?
Perímetro:
6*3 = 18cm
Área:
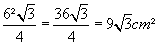
2) Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio?
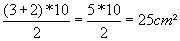
3) Determine a área das seguintes figuras (em cm):
| a) | b) |
| c) | d) |
| e) | |
Retângulo amarelo:
2*3 = 6
Retângulo verde:
2*6 = 12
Retângulo azul:
10*3 = 30
A soma de todos eles:
6 + 12 + 30 = 48cm²
Resposta b:
Área do triângulo:
(3*3)/2 = 4,5
Retângulo laranja:
4* (3+3) = 24
Retângulo rosa:
2*5 = 10
A soma de todas figuras:
4,5 + 24 + 10 = 38,5cm²
Resposta c:
Área do trapézio:
(15 + 10) * 6/2
25*6/2 =
150/2 = 75
Área do retângulo:
8*2 = 16
75 + 16 = 91cm²
Resposta d:
(20*15)/2 =
300 / 2 = 150cm²
Resposta e:
Figura azul:
4 cm
Se observarmos bem, vemos que a parte de baixo da figura roxa se encaixa na parte branca de cima da figura. Logo, temos um retângulo
4*2 = 8
4 + 8 = 12cm²
4) Num losango, a medida da diagonal maior é o dobro da medida da diagonal menor. Sabendo que D = 50cm, qual será a medida da área desse losango?
Solução:
Sabemos que a diagonal maior é o dobro da diagonal menor. Como D = 50cm, podemos afirmar que d = 25cm. Conhecidas as medidas das diagonais, basta utilizar a fórmula da área.
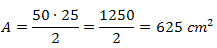
Portanto, o losango tem 625 cm2 de área.
5) Calcular a área de um círculo circunscrito em um triângulo equilátero de lados medindo 18 cm.
Solução:
Na figura ao lado, seja a o apótema, r o raio e h a altura do triângulo então;
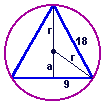

h = a + r
182 = h2 + 92
h = R[324 - 81] = R[243] = 9 R[3]
r2 = 92 + (h-r)2
r2 = 81 + h2 - 2.h.r + r2
81 + 243 - 2.9 R[3].r = 0
r = 18/R[3]
Área do círculo = pi.r2 = 108 pi cm2

DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...
Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de
DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR
- área Do Quadrado Questões Vestibular
Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S= 36 cm Quando dispomos da medida das diagonais do quadrado,...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...
- Retângulo Questões Vestibular
O retângulo é um quadrilátero, pois possui 4 lados que podem ou não ser iguais. Quando os lados forem diferentes ela continua recebendo o nome de retângulo, agora quando os 4 lados forem iguais o retângulo poderá ser chamado de quadrado. O cálculo...
- área Do Quadrado Questões Vestibular
Artigo sobre área do quadrado com questões de fixação. Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S=...
- área Do Losango Questões Vestibular
Artigo sobre como calcular a área de um losango com exercícios para melhor fixação do conteúdo. Losango é uma figura plana conhecida como quadrilátero, possuindo assim duas diagonais e quatro lados congruentes. O seu diferencial com relação às...
