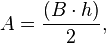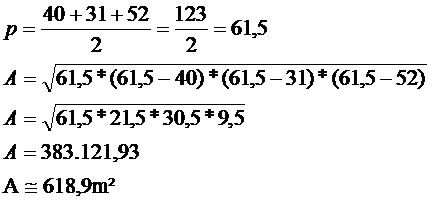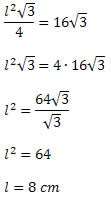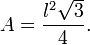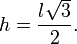Resolução:
Sendo o triângulo retângulo de hipotenusa "a", catetos "b" e "c" e altura relativa à hipotenusa "h". Se sabemos seu perímetro:
a + b + c = 2p
Elevando tudo ao quadrado:
a + b + c = 2p
a2 + b2 + c2 + 2ab + 2bc + 2ac = 4p2
Pelo teorema de Pitágoras b2 + c2 = a2, então:
a2 + b2 + c2 + 2ab + 2bc + 2ac = 4p2
a2 + a2 + 2ab + 2bc + 2ac = 4p2
Chamando a área do triângulo de A, que é a base vezes a altura sobre 2:
ah/2 = A
a = 2A/h
Ou então a área pode ser o produto dos catetos sobre 2:
bc/2 = A
bc = 2A
Então podemos continuar usando isso:
a2 + a2 + 2ab + 2bc + 2ac = 4p2
2a2 + 2ab + 2bc + 2ac = 4p2
2a2 + 2ab + 4A + 2ac = 4p2
2a2 + 2a.(b + c) + 4A = 4p2
E aqui vamos achar que como a + b + c = 2p:
a + b + c = 2p
b + c = 2p - a
Colocando isso também na equação e no lugar de "a" colocando sempre 2A/h:
2a2 + 2a.(b + c) + 4A = 4p2
2a2 + 2a.(2p - a) + 4A = 4p2
2(2A/h)2 + 2(2A/h).(2p - 2A/h) + 4A = 4p2
Agora você tem uma equação só com A e p, que você pode simplificar tirando o mínimo que é h2, até achar:
2Ap + Ah - p2h = 0
A.(h + 2p) = p2h
A = p2h/(h + 2p)
6) Um triângulo equilátero possui área de 16?3 cm². Determine a medida do lado desse triângulo.