Vestibular
Chama-se equação linear a n incógnitas a toda equação do tipo:
a1 x1 + a2x2 +a3x3 + ... + anxn = b
onde:
6x ? 2y ? 2z + w = 6
onde o par (1,2) é a única solução de ambos
S1 2 * 1 + 3 *2 = 8 e S2 2 * 1 + 3 * 2 = 8
5 * 1 - 2 * 2 = 1 3 * 1 - 5 * 2 = - 7
Dizemos então que os sistemas S1 e S2 são equivalentes, pois possuem o mesmo conjunto solução.
Em geral:
Dois sistemas S1 e S2 são equivalentes se toda solução de S1 for também solução de S2 e vice-versa.
4 - Se o sistema de equações é COMPATÍVEL e possui apenas uma solução, dizemos que ele é DETERMINADO.

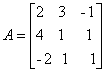
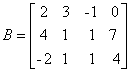
Imagina-se que o sistema é uma matriz da qual se deve encontrar o determinante.
Deve-se achar o determinante D dado por:
que é o dos coeficientes das incógnitas.
Para o determinante de x substituem-se seus coeficientes pelos termos independentes, logo:
E analogamente para y:
Segundo a regra de Cramer:
Dado o sistema linear
Veja também:
 Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?
Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?
E aproveite as Ferramentas de estudo.
 Um jeito mais fácil de treinar sua escuta e sua fala em inglês.
Um jeito mais fácil de treinar sua escuta e sua fala em inglês.
Como melhorar sua conversação rapidamente.
Como aprender a falar e entender sem ficar estudando gramática.
Inglês para negócios e áreas especificas.
 Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.
vá ao site:
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Determinantes: Propriedades E Teorema De Laplace
As dificuldades que podem ocorrer no cálculo de determinantes dependem naturalmente da ordem e dos elementos da matriz considerada. As propriedades que estudaremos a seguir poderão ajudar na simplificação desse cálculo. Primeira propriedade Se...
- Determinantes (regra De Saurus, Cofator)
Inicialmente, iremos introduzir algumas regras que permitam o cálculo de determinantes nos casos particulares da matriz quadrada de ordem 1, 2 ou 3 e, a seguir, após o domínio dessas regras, apresentaremos uma definição geral para determinantes de...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
Vestibular
Sistemas de equações lineares (Regra de Cramer, matriz de um sistema linear)
Chama-se equação linear a n incógnitas a toda equação do tipo:
a1 x1 + a2x2 +a3x3 + ... + anxn = b
onde:
- a1, a2, a3, ..., an são números reais quaisquer chamados coeficientes;
- x1, x2, x3, ... xn são as incógnitas;
- b é o termo independente.
A equação 2x + 5y - 6z = 10 é um exemplo de equação linear, onde:
- os coeficientes são 2, 5 e -6;
- as incógnitas são x, y, z;
- o termo independente é 10.
Vejamos outros exemplos de equações lineares:
a) x + y = 3 b) 3x - 2y = 7 c) x + 2y - z = 2
Resolução de uma equação linear
Considere a equação x + 2y + 3z = 11.
- Para x = 2, y = 3 e z = 1, teremos 2 + 2 * (3) + 3 * (1) = 11; logo, a terna (2,3,1) é uma solução da equação.
- Para x = 3, y = 2, e z = 5, teremos: 3 + 2 * (2) + 3 * (5) ? 11; logo, a terna (3,2,5) não é solução da equação.
Assim, um determinado conjunto será a solução da equação linear se todos os elementos desse conjunto forem iguais às incógnitas da equação e ao substituirmos os elementos desse conjunto nas incógnitas da equação linear a igualdade
a1 x1 + a2x2 +a3x3 + ... + anxn = b deve ser verdadeira.
a1 x1 + a2x2 +a3x3 + ... + anxn = b deve ser verdadeira.
Vejamos alguns exemplos:
Ex1: Dado o conjunto solução (2, 5, 3) e a equação linear 3x + 2y - 5z = 1 verificar se é verdadeira essa solução.
Para resolução da questão deve-se substituir os valores 2, 5 e 3 nas suas respectivas incógnitas.
3 * 2 + 2 * 5 - 5 * 3 = 1
6 + 10 - 15 = 1
1 = 1, como a igualdade é verdadeira, podemos concluir que o conjunto solução (2, 5, 3) é solução da equação
3x + 2y - 5z = 1.
Sistemas de equações lineares
Chama-se sistema linear a todo sistema formado por equações lineares.
Assim, o sistema S1 x + y = 3 é um sistema linear de duas equações com duas incógnitas.
x ? y = 1
O sistema S2 x ? 2y ? z + w = 12 é um sistema linear de três equações com quatro incógnitas.
5x + 3y + 5z ? w = 3Assim, o sistema S1 x + y = 3 é um sistema linear de duas equações com duas incógnitas.
x ? y = 1
6x ? 2y ? 2z + w = 6
Nota:
3- Consideremos os sistemas:
S1 2x + 3y = 8 e S2 2x + 3y = 8
5x - 2y = 1 3x - 5y = -7
1- Se um sistema de equações possuir pelo menos uma solução, dizemos que ele é POSSÍVEL ou COMPATÍVEL.
2 - Se um sistema de equações não possuir solução, dizemos que ele é IMPOSSÍVEL ou INCOMPATÍVEL.
3- Consideremos os sistemas:
S1 2x + 3y = 8 e S2 2x + 3y = 8
5x - 2y = 1 3x - 5y = -7
onde o par (1,2) é a única solução de ambos
S1 2 * 1 + 3 *2 = 8 e S2 2 * 1 + 3 * 2 = 8
5 * 1 - 2 * 2 = 1 3 * 1 - 5 * 2 = - 7
Dizemos então que os sistemas S1 e S2 são equivalentes, pois possuem o mesmo conjunto solução.
Em geral:
Dois sistemas S1 e S2 são equivalentes se toda solução de S1 for também solução de S2 e vice-versa.
4 - Se o sistema de equações é COMPATÍVEL e possui apenas uma solução, dizemos que ele é DETERMINADO.
5 - Se o sistema de equações é COMPATÍVEL e possui mais de uma solução, dizemos que ele é INDETERMINADO.
6 - Se todos os termos independentes de um sistema linear S forem nulos, ou seja, b1 = b2 = b3 = ... = bn = 0, o sistema é chamado homogêneo.
Exemplo: o sistema S1 4x + 2y - z = 0 é um sistema linear homogêneo e a terna (0, 0, 0) é uma solução de
x - y + 2z = 0
x = y - z = 0
S1. Se existirem outras soluções, estas serão chamadas soluções não-triviais. A terna (-1, 3, 2) é uma solução não-trivial de S1.
Matrizes de um sistema linear
a) Matriz incompleta: a matriz A formada pelos coeficientes das variáveis.
Em relação ao sistema:

a matriz incompleta é:
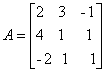
b) Matriz completa: matriz B que se obtém adicionando à matriz incompleta uma última coluna formada pelos termos independentes das equações do sistema.
Assim, para o mesmo sistema acima, a matriz completa é:
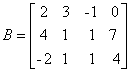
Regra de Cramer
É uma regra prática que permite a resolução de um sistema de equações lineares de n equações e n incógnitas.
 |
Deve-se achar o determinante D dado por:
 |
que é o dos coeficientes das incógnitas.
Para o determinante de x substituem-se seus coeficientes pelos termos independentes, logo:
 |
E analogamente para y:
 |
Segundo a regra de Cramer:
 |
 |
Exemplo resolvido:
Dado o sistema linear 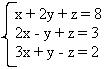 , quais os valores de x, y e z.
, quais os valores de x, y e z.
resolução:
Devemos encontrar a matriz incompleta desse sistema linear que será chamada de A.
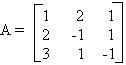
. Agora calculamos o seu determinante que será representado por D.
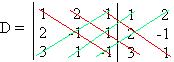
D = 1 + 6 + 2 + 3 ? 1 + 4
D = 15.
Agora devemos substituir os temos independentes na primeira coluna da matriz A, formando assim uma segunda matriz que será representada por Ax.
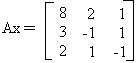
. Agora calcularmos o seu determinante representado por Dx.
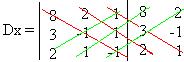
Dx = 8 + 4 + 3 + 2 ? 8 + 6
Dx = 15
Substituímos os termos independentes na segunda coluna da matriz incompleta formando a matriz Ay.

. Agora calcularmos o seu determinante Dy.

Dy = -3 + 24 +4 ? 9 ? 2 + 16
Dy = 30
Substituindo os termos independentes do sistema na terceira coluna da matriz incompleta formaremos a matriz Az.

. Agora calculamos o seu determinante representado por Dz.
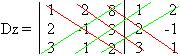
Depois de substituir todas as colunas da matriz incompleta pelos termos independentes, iremos colocar em prática a regra de Cramer.
A incógnita x = Dx = 15 = 1
D 15
A incógnita y = Dy = 30 = 2
D 15
A incógnita z = Dz = 45 = 3
D 15
Assim, o conjunto solução desse sistema será V = {(1,2,3)}.
. Agora calculamos o seu determinante que será representado por D.
D = 1 + 6 + 2 + 3 ? 1 + 4
D = 15.
Agora devemos substituir os temos independentes na primeira coluna da matriz A, formando assim uma segunda matriz que será representada por Ax.
. Agora calcularmos o seu determinante representado por Dx.
Dx = 8 + 4 + 3 + 2 ? 8 + 6
Dx = 15
Substituímos os termos independentes na segunda coluna da matriz incompleta formando a matriz Ay.
. Agora calcularmos o seu determinante Dy.
Dy = -3 + 24 +4 ? 9 ? 2 + 16
Dy = 30
Substituindo os termos independentes do sistema na terceira coluna da matriz incompleta formaremos a matriz Az.
. Agora calculamos o seu determinante representado por Dz.
Depois de substituir todas as colunas da matriz incompleta pelos termos independentes, iremos colocar em prática a regra de Cramer.
A incógnita x = Dx = 15 = 1
D 15
A incógnita y = Dy = 30 = 2
D 15
A incógnita z = Dz = 45 = 3
D 15
Assim, o conjunto solução desse sistema será V = {(1,2,3)}.
Determinantes (regra de Saurus, cofator)
Exercícios Determinantes vestibular
Determinantes: propriedades e Teorema de LaPlace
Questões Fuvest matemática de vestibulares anteriores
Curso de Inglês Download - ONELAND Rápido
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês.
Metodologia Comunicativa
 Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?
Descubra como é possível conseguir falar com excelente fluência, rapidez e facilidade sem ter que ficar se matriculando em curso e comprando aqueles livros importados e caríssimos?E aproveite as Ferramentas de estudo.
Professores Nativos
 Um jeito mais fácil de treinar sua escuta e sua fala em inglês.
Um jeito mais fácil de treinar sua escuta e sua fala em inglês.Como melhorar sua conversação rapidamente.
Como aprender a falar e entender sem ficar estudando gramática.
Inglês para negócios e áreas especificas.
Diferenciais ONELAND.
 Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.
Vamos ensinar-lhe alguns truques que passamos para os nossos alunos para atingir um alto nível de fluência em inglês. O vocabulário deste curso inclui vários grupos, entre eles: datas, meses, horas, cores, objetos comuns, roupas, família, pessoas, lugares, países, comida e compras etc.http://cursodeinglesdownload.net/
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Determinantes: Propriedades E Teorema De Laplace
As dificuldades que podem ocorrer no cálculo de determinantes dependem naturalmente da ordem e dos elementos da matriz considerada. As propriedades que estudaremos a seguir poderão ajudar na simplificação desse cálculo. Primeira propriedade Se...
- Determinantes (regra De Saurus, Cofator)
Inicialmente, iremos introduzir algumas regras que permitam o cálculo de determinantes nos casos particulares da matriz quadrada de ordem 1, 2 ou 3 e, a seguir, após o domínio dessas regras, apresentaremos uma definição geral para determinantes de...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
