Vestibular
As dificuldades que podem ocorrer no cálculo de determinantes dependem naturalmente da ordem e dos elementos da matriz considerada. As propriedades que estudaremos a seguir poderão ajudar na simplificação desse cálculo.
Primeira propriedade
Se os elementos de uma fila de uma matriz quadrada forem iguais a zero, seu determinante será nulo.
Segunda propriedade
O determinante de uma matriz é igual ao determinante de sua transposta.
det R=det Rt
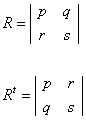
det R = ps -- qr
det Rt = ps ? rq
Terceira propriedade
Se uma matriz quadrada tem duas filas paralelas iguais, seu determinante será nulo.
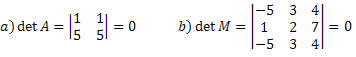
Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
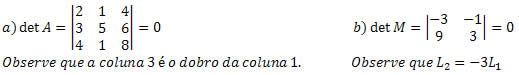
Quinta propriedade
Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.

Os elementos da 1ª linha de P foram multiplicados por 2, então: det P? = 2 * det P
Sexta propriedade
Quando trocamos duas colunas ou duas linhas de posição de uma matriz, o valor do seu determinante será oposto ao determinante da anterior.

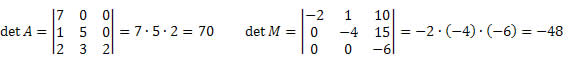

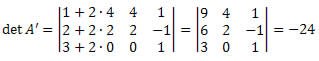
Nona propriedade
Décima propriedade
Teorema de laPlace
Consiste num método de cálculo do determinante de matrizes quadradas de ordem n ? 2 utilizando o cofator.
Lembre-se: o cofator do elemento aij de uma matriz quadrada é: 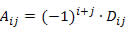
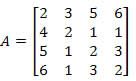

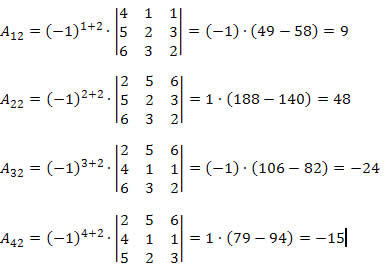
Veja também:
- Propriedades Dos Logaritmos Com Exemplos
É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição: O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma: logab = x ? ax =...
- Triângulo De Pascal E Suas Propriedades
Nesse artigo, estudaremos o triângulo de Pascal e suas propriedades com exercícios resolvidos O triângulo de Pascal recebeu esse nome devido ao matemático Blaise Pascal (1623-1662). O triângulo é infinito e simétrico, e seus lados esquerdo...
- Sistemas De Equações Lineares (regra De Cramer, Matriz De Um Sistema Linear)
Chama-se equação linear a n incógnitas a toda equação do tipo: a1 x1 + a2x2 +a3x3 + ... + anxn = b onde: a1, a2, a3, ..., an são números reais quaisquer chamados coeficientes;x1, x2, x3, ... xn são as incógnitas;b...
- Exercícios Determinantes Vestibular
Aqui vai uma lista de questões sobre determinantes para que você se prepare para o vestibular. 01. (Unicamp - SP) Seja a um número real e seja:a) Para a=1, encontre todas as raízes da equação p(x)=0b) Encontre os valores de a para os quais...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
Vestibular
Determinantes: propriedades e Teorema de LaPlace
As dificuldades que podem ocorrer no cálculo de determinantes dependem naturalmente da ordem e dos elementos da matriz considerada. As propriedades que estudaremos a seguir poderão ajudar na simplificação desse cálculo.
Primeira propriedade
Se os elementos de uma fila de uma matriz quadrada forem iguais a zero, seu determinante será nulo.
Exemplo:
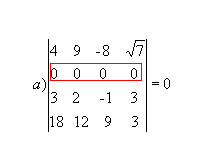 | 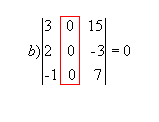 |
Segunda propriedade
O determinante de uma matriz é igual ao determinante de sua transposta.
det R=det Rt
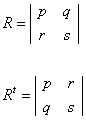
det R = ps -- qr
det Rt = ps ? rq
Terceira propriedade
Se uma matriz quadrada tem duas filas paralelas iguais, seu determinante será nulo.
Exemplo:
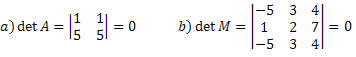
Quarta propriedade
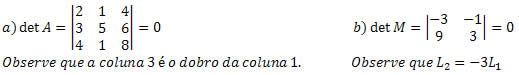
Quinta propriedade
Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.

Os elementos da 1ª linha de P foram multiplicados por 2, então: det P? = 2 * det P
Sexta propriedade
Quando trocamos duas colunas ou duas linhas de posição de uma matriz, o valor do seu determinante será oposto ao determinante da anterior.
Exemplo:

Sétima propriedade
O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.
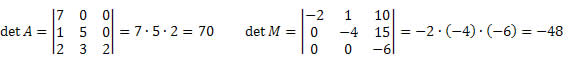
Oitava propriedade
Teorema de Jacobi: Um determinante não se altera quando somamos a uma fila outra fila paralela multiplicada por um número real qualquer.
Exemplo:

Se somarmos os elementos da coluna 1 com o dobro dos elementos da coluna 2, o determinante não irá se alterar.
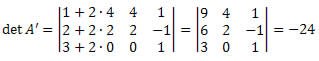
Nona propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.
Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kn.
det (k*A) = kn * det A
det (k*A) = kn * det A
Teorema de laPlace
Consiste num método de cálculo do determinante de matrizes quadradas de ordem n ? 2 utilizando o cofator.
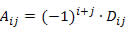
Para aplicar o teorema de la place devemos escolher qualquer fila (linha ou coluna) da matriz B e multiplicar cada elemento da fila pelo seu respectivo cofator. O resultado da matriz B será a soma dos produtos dos elementos da fila pelos seus respectivos cofatores.
Calcule o determinante da matriz a seguir utilizando o Teorema de Laplace.
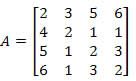
Solução: Devemos escolher uma linha ou uma coluna da matriz A.
Se escolhermos a coluna 2, teremos:
Se escolhermos a coluna 2, teremos:

Pelo teorema de Laplace, sabemos que:
D = a12?A12 + a22?A22 + a32?A32 + a42?A42
Segue que:
D = a12?A12 + a22?A22 + a32?A32 + a42?A42
Segue que:
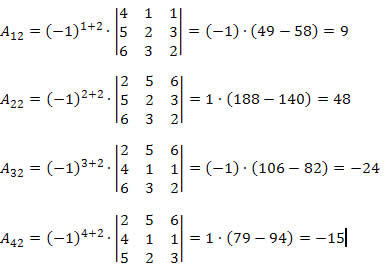
Assim, o determinante da matriz A será:
D = 3?9 + 2?48 + 1?(-24) + 1?(-15) = 27 + 96 - 24 - 15 = 84
D = 3?9 + 2?48 + 1?(-24) + 1?(-15) = 27 + 96 - 24 - 15 = 84
Veja também:
Determinantes (regra de Saurus, cofator)
Exercícios Determinantes vestibular
Sistemas de equações lineares (Regra de Cramer, matriz de um sistema linear)
Exercícios Determinantes vestibular
- Propriedades Dos Logaritmos Com Exemplos
É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição: O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma: logab = x ? ax =...
- Triângulo De Pascal E Suas Propriedades
Nesse artigo, estudaremos o triângulo de Pascal e suas propriedades com exercícios resolvidos O triângulo de Pascal recebeu esse nome devido ao matemático Blaise Pascal (1623-1662). O triângulo é infinito e simétrico, e seus lados esquerdo...
- Sistemas De Equações Lineares (regra De Cramer, Matriz De Um Sistema Linear)
Chama-se equação linear a n incógnitas a toda equação do tipo: a1 x1 + a2x2 +a3x3 + ... + anxn = b onde: a1, a2, a3, ..., an são números reais quaisquer chamados coeficientes;x1, x2, x3, ... xn são as incógnitas;b...
- Exercícios Determinantes Vestibular
Aqui vai uma lista de questões sobre determinantes para que você se prepare para o vestibular. 01. (Unicamp - SP) Seja a um número real e seja:a) Para a=1, encontre todas as raízes da equação p(x)=0b) Encontre os valores de a para os quais...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
