Vestibular
Inicialmente, iremos introduzir algumas regras que permitam o cálculo de determinantes nos casos particulares da matriz quadrada de ordem 1, 2 ou 3 e, a seguir, após o domínio dessas regras, apresentaremos uma definição geral para determinantes de uma matriz quadrada de ordem n.
Determinante de uma matriz quadrada de 1ª ordem
O determinante da matriz A = | a11|, indicado por det A ou |a11|, é o próprio elemento a11, ou seja:
det A = |a11| = a11 (não confundir com o módulo do número a11).
Exs: Se A = [-3], então det A = |-3|.
Se B = [6], então det A = |6| = 6
Determinante de uma matriz quadrada de 2ª ordem
O determinante da matriz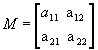 é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
Veja o exemplo abaixo:
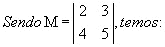
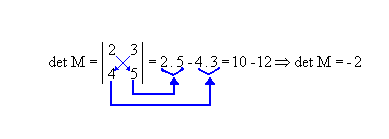
 , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31:
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- ângulos Complementares E Suplementares Questões Resolvidas
COMPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 90º e neste caso, um ângulo é o complemento do outro. Ex.: 30o e 50o (30+50=90) ou37o e 53o (37+53=90) ou20o e 70o (20+70=90) ... SUPLEMENTARES:...
- Sistemas De Equações Lineares (regra De Cramer, Matriz De Um Sistema Linear)
Chama-se equação linear a n incógnitas a toda equação do tipo: a1 x1 + a2x2 +a3x3 + ... + anxn = b onde: a1, a2, a3, ..., an são números reais quaisquer chamados coeficientes;x1, x2, x3, ... xn são as incógnitas;b...
- Exercícios Determinantes Vestibular
Aqui vai uma lista de questões sobre determinantes para que você se prepare para o vestibular. 01. (Unicamp - SP) Seja a um número real e seja:a) Para a=1, encontre todas as raízes da equação p(x)=0b) Encontre os valores de a para os quais...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
Vestibular
Determinantes (regra de Saurus, cofator)
Inicialmente, iremos introduzir algumas regras que permitam o cálculo de determinantes nos casos particulares da matriz quadrada de ordem 1, 2 ou 3 e, a seguir, após o domínio dessas regras, apresentaremos uma definição geral para determinantes de uma matriz quadrada de ordem n.
Determinante de uma matriz quadrada de 1ª ordem
O determinante da matriz A = | a11|, indicado por det A ou |a11|, é o próprio elemento a11, ou seja:
det A = |a11| = a11 (não confundir com o módulo do número a11).
Exs: Se A = [-3], então det A = |-3|.
Se B = [6], então det A = |6| = 6
Determinante de uma matriz quadrada de 2ª ordem
O determinante da matriz
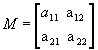 é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.Veja o exemplo abaixo:
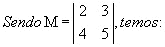
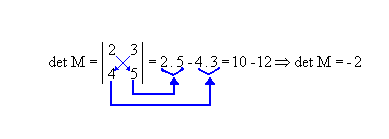
Determinante de uma matriz de 3ª ordem
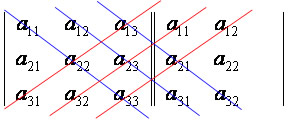
O cálculo do determinante de uma matriz quadrada de ordem 3 pode ser calculado usando a regra de Saurus, que consiste no seguinte:
- copia-se o determinante repetindo-se as duas primeiras colunas;
- multiplicam-se os elementos ligados por "traços vermelhos", mantendo-se o sinal de cada produto;
- multiplicam-se os elementos ligados por "traços azuis", trocando-se o sinal de cada produto;
- somam-se os resultados obtidos.

Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} ? {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21* a33)}
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} ? {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21* a33)}
Exemplo :
Dada a matriz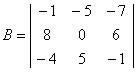 , calcule o seu determinante.
, calcule o seu determinante.
Diagonais principais
(?1) * 0 * (?1) = 0
(?5) * 6 * (?4) = 120
(?7) * (8) * (5) = ? 280
0 + 120 + (?280)
120 ? 280
? 160
Diagonais secundárias
(?7) * 0 * (?4) = 0
(?1) * 6 * 5 = ? 30
(?5) * 8 * (?1) = 40
0 + (?30) + 40
?30 +40
10
Determinante
DB = ?160 ? 10
DB = ? 170
Dada a matriz
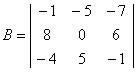 , calcule o seu determinante.
, calcule o seu determinante.Diagonais principais
(?1) * 0 * (?1) = 0
(?5) * 6 * (?4) = 120
(?7) * (8) * (5) = ? 280
0 + 120 + (?280)
120 ? 280
? 160
Diagonais secundárias
(?7) * 0 * (?4) = 0
(?1) * 6 * 5 = ? 30
(?5) * 8 * (?1) = 40
0 + (?30) + 40
?30 +40
10
Determinante
DB = ?160 ? 10
DB = ? 170
Matriz Cofator
consideremos uma matriz quadrada A, de ordem n(n ? 2), e um elemento aij de A. Chama-se cofator do elemento aij ao produto de (-1)i+j pelo determinante da matriz obtida, quando se elimina em A a linha i e a coluna j.
Exemplo:
Sendo  , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31: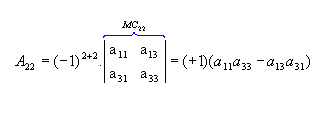 |
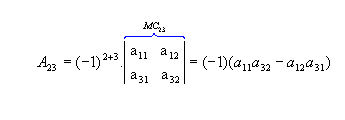 |
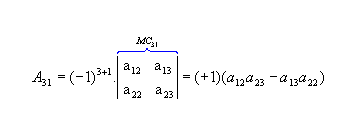 |
Veja também:
Determinantes: propriedades e Teorema de LaPlace
Exercícios Determinantes vestibular
Sistemas de equações lineares (Regra de Cramer, matriz de um sistema linear)
matrizes exercícios - matemática vestibular
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- ângulos Complementares E Suplementares Questões Resolvidas
COMPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 90º e neste caso, um ângulo é o complemento do outro. Ex.: 30o e 50o (30+50=90) ou37o e 53o (37+53=90) ou20o e 70o (20+70=90) ... SUPLEMENTARES:...
- Sistemas De Equações Lineares (regra De Cramer, Matriz De Um Sistema Linear)
Chama-se equação linear a n incógnitas a toda equação do tipo: a1 x1 + a2x2 +a3x3 + ... + anxn = b onde: a1, a2, a3, ..., an são números reais quaisquer chamados coeficientes;x1, x2, x3, ... xn são as incógnitas;b...
- Exercícios Determinantes Vestibular
Aqui vai uma lista de questões sobre determinantes para que você se prepare para o vestibular. 01. (Unicamp - SP) Seja a um número real e seja:a) Para a=1, encontre todas as raízes da equação p(x)=0b) Encontre os valores de a para os quais...
- Matrizes (operações) Exercícios
Nesse artigo será abordado operações com matrizes, tipos de matrizes e alguns exercicios de vestibulares passados para fixação da matéria e preparação para o vestibular. Matrizes As matrizes são estruturas matemáticas organizadas na forma...
