Vestibular
É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição:
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ? ax = b
Exemplos: log39 ? 32 = 9
log10100 ? 102 = 100
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x ? ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ? b = c
Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
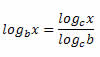 Essa propriedade é utilizada quando o logaritmo a ser calculado apresenta uma base que torna os cálculos mais complexos, e ela nos permite escolher a base que seja mais conveniente, tornando os cálculos mais simples. A propriedade da mudança de base também é fundamental para a simplificação de expressões que envolvem logaritmos com bases diferentes.
Essa propriedade é utilizada quando o logaritmo a ser calculado apresenta uma base que torna os cálculos mais complexos, e ela nos permite escolher a base que seja mais conveniente, tornando os cálculos mais simples. A propriedade da mudança de base também é fundamental para a simplificação de expressões que envolvem logaritmos com bases diferentes.
Exemplo: Se desejarmos calcular o valor do seguinte logaritmo log5 11, nem com uso de uma calculadora científica seria possível, pois ela trabalha com logaritmos na base 10 ou na base e. Nesse caso, seria necessário fazer a mudança para uma dessas bases. Assim, teremos:
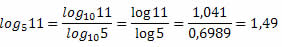
- Radiciação Propriedades Dos Radicais
Artigo sobre radiciação e as propriedades dos radicais. O tópico em questão agora é a radiciação que é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões...
- Potência Fracionária Questões
A regra é simples, o numerador do expoente será o expoente do radicando e o denominador do expoente é o índice do radical. Tem-se: Exemplos: não representa um número pois não é um número (!)Exercícios 1) Calcule .Solução:Podemos...
- Propriedades Das Potências
Artigo sobre potenciação: propriedades das potências, potência fracionária, potência de base 10, potência de base zero, potenciação de números racionais e potenciação de monômios As principais operações são: adição, subtração, divisão...
- Números Complexos Exercícios E Teoria
Artigo sobre números complexos com exercícios e teoria: propriedades do conjugado, operações, conjugado e potência de um número complexo. PROPRIEDADES Definição: O conjugado de um complexo Ex: Propriedade 1: A soma...
- Equações Logarítmicas: Aprenda Como Resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base. Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos: logbx = logby, onde x = y logbx...
Vestibular
Propriedades dos logaritmos com exemplos
É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição:
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ? ax = b
Exemplos: log39 ? 32 = 9
log10100 ? 102 = 100
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x ? ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ? b = c
Esta propriedade é muito utilizada na solução de exercícios envolvendo equações onde aparecem logaritmos (equações logarítmicas).
O logaritmo de um produto é igual a soma dos logaritmos dos fatores
loga(b.c) = log a b + log a b
Observe que
log2 (8.4) = log2 (32) = 5
log2 (8.4) = log2 (32) = 5
O logaritmo de um quociente é igual a subtração dos logaritmos do numerador e do denominador.
loga(b/c) = log a b - log a b
Observe que
log2 (8/4) = log2 (2) = 1
log2 (8/4) = log2 (2) = 1
O logaritmo de uma potência é igual a multiplicação do expoente pelo logaritmo da base.
loga(bc) = c. log a b
Observe que
log2 (25) = log2 (32) = 5
log2 (25) = log2 (32) = 5
Propriedade da mudança de base.
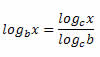
Exemplo: Se desejarmos calcular o valor do seguinte logaritmo log5
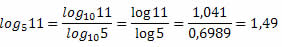
Os cálculos dos logaritmos, após a mudança de base, foram feitos com o auxílio de uma calculadora científica.
Exemplos:
a)logx8 = 2 ? x2 = 8 ? ?x = ?8 ? x = 2?2
b)log4(2x ? 1) = 1/2 ? 2x ? 1 = 41/2 ? 2x ? 1 = ?4 ? 2x ? 1 = 2 ? 2x = 3 ? x = 3/2
b)log4(2x ? 1) = 1/2 ? 2x ? 1 = 41/2 ? 2x ? 1 = ?4 ? 2x ? 1 = 2 ? 2x = 3 ? x = 3/2
c) log81x = 3/4 ? x = 813/4 ? x = (34)3/4 ? x = 312/4 ? x = 33 ? x = 27
d) 16log25 = (24)log25 = (2log25)4 = 54 = 625
e) log0,01 = x ? 10x = 0,01 ? 10x = 1/100 ? 10x = 10?2 ? x = ?2
e) log0,01 = x ? 10x = 0,01 ? 10x = 1/100 ? 10x = 10?2 ? x = ?2
f) log(1/100)=Log(10-2)=-2
- Radiciação Propriedades Dos Radicais
Artigo sobre radiciação e as propriedades dos radicais. O tópico em questão agora é a radiciação que é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões...
- Potência Fracionária Questões
A regra é simples, o numerador do expoente será o expoente do radicando e o denominador do expoente é o índice do radical. Tem-se: Exemplos: não representa um número pois não é um número (!)Exercícios 1) Calcule .Solução:Podemos...
- Propriedades Das Potências
Artigo sobre potenciação: propriedades das potências, potência fracionária, potência de base 10, potência de base zero, potenciação de números racionais e potenciação de monômios As principais operações são: adição, subtração, divisão...
- Números Complexos Exercícios E Teoria
Artigo sobre números complexos com exercícios e teoria: propriedades do conjugado, operações, conjugado e potência de um número complexo. PROPRIEDADES Definição: O conjugado de um complexo Ex: Propriedade 1: A soma...
- Equações Logarítmicas: Aprenda Como Resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base. Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos: logbx = logby, onde x = y logbx...
