Vestibular
Artigo sobre números complexos com exercícios e teoria: propriedades do conjugado, operações, conjugado e potência de um número complexo.

Dado os números z1 = 3 ? i e z2 = -5 + 4i. Somando os dois teremos:
z1 + z2 = (3? i) + (-5 + 4i)
z1 + z2 = 3- i ? 5 + 4i
z1 + z2 = 3 ? 5 ? i + 4i
z1 + z2 = - 2 + 3i
Dado os números z1 =(5 + 8i) e z2= (1 + 2i). Subtraindo os dois teremos:
z1 - z2 = (5 ? 8i) - (1 + 2i)
Podemos concluir que para subtrair ou adicionar números complexos devemos operar parte real com parte real e parte imaginária com parte imaginária.
Os números complexos são multiplicados com base na propriedade distributiva, sempre lembrando que um numeral complexo é formado por uma parte real e uma imaginária.

Como sabemos, i² = ? 1.
Logo,
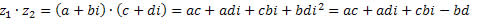
Agrupando os termos semelhantes, obtemos:
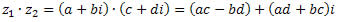
a) (4 + 3i) * (2 + 6i) b) (1+2i)?(2-3i) = [1?2 - 2?(-3)] + [1?(-3) + 2?2]i
(1+2i)?(2-3i) = (2+6) + (-3+4)i = 8 + i
Para realizar a divisão de dois números complexos precisamos introduzir o conceito de conjugado de um número complexo. Seja z = a + bi, o conjugado de z é z = a - bi. Agora podemos definir a operação de divisão para números complexos.
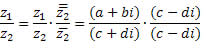

 Para realizar o produto no denominador vamos recorrer aos produtos notáveis, mais especificamente ao produto da soma pela diferença de dois termos, onde temos que:
Para realizar o produto no denominador vamos recorrer aos produtos notáveis, mais especificamente ao produto da soma pela diferença de dois termos, onde temos que:



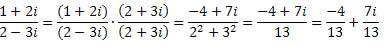
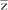 = a ? bi.
= a ? bi.



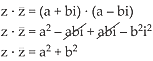



Observe que na potência de i com expoente 4 os valores começam a se repetir e o mesmo acontece nas potências com expoentes 8 e 12, caracterizando um padrão de repetição no cálculo dessas potências. Como os valores se repetem a cada quatro potências calculadas, ou seja, de 4 em 4, podemos obter o valor de qualquer potência de i utilizando o seguinte método:
Por exemplo, se desejamos calcular o valor de i 125.
Faremos a divisão de 125 por 4:
Exercícios números complexos
1) (PUC-MG) Qualo é o quociente de (8 + i)/(2 - i) é igual a
3) (Mackenzie-SP) O valor da expressão y = i + i2 + i3 + ... + i1001 é:
a) i² b) i c) i³ d) i² + 1 e) i +1
4) (UCSal) Para que o produto (a + i).(3 - 2i) seja real, a deve ser:
a) 2/3 b) 4/3 c) 3/2 d) 3/4 e) 3/5
- Polinômios Questões Vestibular
Adição e subtração de polinômios O procedimento utilizado na adição e subtração de polinômios envolve técnicas de redução de termos semelhantes, operações envolvendo sinais iguais e sinais diferentes e jogo de sinal. Observe os exemplos:...
- Múltiplos E Divisores De Um Numero Natural Questões E Teoria
Artigo sobre múltiplos e divisores de um número natural com questões de fixação. Divisor de um número natural Um número é divisor de outro quando o resto da divisão for igual a 0. Portanto, 12 é divisível por 1, 2, 3, 4, 6 e 12. 36 é divisível...
- Números Inteiros Questões
Conjunto dos números inteiros Pertencem ao conjunto dos números inteiros, os números negativos e também o Conjunto dos Números Naturais. Os números positivos são opostos aos números negativos e os negativos opostos aos positivos. Sua...
- Radiciação Propriedades Dos Radicais
Artigo sobre radiciação e as propriedades dos radicais. O tópico em questão agora é a radiciação que é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões...
- Propriedades Das Potências
Artigo sobre potenciação: propriedades das potências, potência fracionária, potência de base 10, potência de base zero, potenciação de números racionais e potenciação de monômios As principais operações são: adição, subtração, divisão...
Vestibular
números complexos exercícios e teoria
Artigo sobre números complexos com exercícios e teoria: propriedades do conjugado, operações, conjugado e potência de um número complexo.
PROPRIEDADES
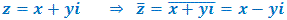 Definição: O conjugado de um complexo
Definição: O conjugado de um complexo
Ex:
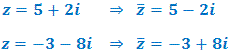
Propriedade 1: A soma de 2 complexos conjugados é sempre um número real.

Propriedade 2: O produto de 2 complexos conjugados é sempre um número positivo.
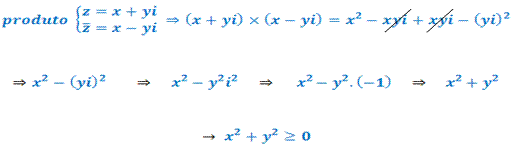
Propriedade 3: O conjugado do conjugado , de um complexo, é o próprio complexo.
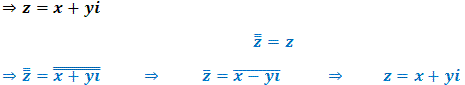
Propriedade 4: O conjugado da soma, é igual a soma dos conjugados.

Propriedade 5: O conjugado do produto, é igual ao produto dos conjugados.
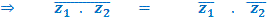
Ex:
Propriedade 1: A soma de 2 complexos conjugados é sempre um número real.
Propriedade 2: O produto de 2 complexos conjugados é sempre um número positivo.
Propriedade 3: O conjugado do conjugado , de um complexo, é o próprio complexo.
Propriedade 4: O conjugado da soma, é igual a soma dos conjugados.
Propriedade 5: O conjugado do produto, é igual ao produto dos conjugados.
Adição e subtração
A forma algébrica a + bi admite todas as operações, assim como em R, substituindo i2 por -1, sempre que necessário.
z1 + z2 = (3? i) + (-5 + 4i)
z1 + z2 = 3- i ? 5 + 4i
z1 + z2 = 3 ? 5 ? i + 4i
z1 + z2 = - 2 + 3i
Dado os números z1 =(5 + 8i) e z2= (1 + 2i). Subtraindo os dois teremos:
z1 - z2 = (5 ? 8i) - (1 + 2i)
z1 - z2 = 5 - 1 - 8i - 2i
z1 - z2 = 4 + 6i
Podemos concluir que para subtrair ou adicionar números complexos devemos operar parte real com parte real e parte imaginária com parte imaginária.
Multiplicação de números complexos

Como sabemos, i² = ? 1.
Logo,
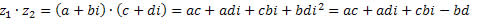
Agrupando os termos semelhantes, obtemos:
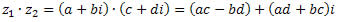
Exemplos:
(1+2i)?(2-3i) = (2+6) + (-3+4)i = 8 + i
8 + 24i + 6i + 18i² (lembrando que i² = ? 1)
8 + 24i + 6i + 18 * (?1)
8 + 24i + 6i ? 18
?10 + 30i
8 + 24i + 6i + 18 * (?1)
8 + 24i + 6i ? 18
?10 + 30i
Divisão de números Complexos
Para realizar a divisão de dois números complexos precisamos introduzir o conceito de conjugado de um número complexo. Seja z = a + bi, o conjugado de z é z = a - bi. Agora podemos definir a operação de divisão para números complexos.
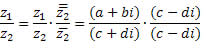
Agora vejamos este exemplo de divisão:
Para começar vamos multiplicar o divisor e o dividendo pelo conjugado do divisor como explicado acima:
Continuando o processo da divisão temos:
Note que inicialmente tínhamos o divisor imaginário 2 - 7i e no final temos o divisor real 53. É por isto que utilizamos o conjugado como expediente para realizar a divisão, assim conseguimos transformar um divisor imaginário em um divisor real, o que facilita muito as coisas, como pudemos ver na passagem do penúltimo para o último passo.
vamos ver outro exemplo:
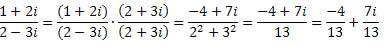
 Conjugado de um Número Complexo  |
Chamamos de conjugado do número complexo
z = a + bi, com a e b reais, o número complexo
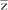 = a ? bi.
= a ? bi.Exemplos

1o) z1 = 2 ? 3i 
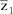 = 2 + 3i
= 2 + 3i

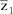 = 2 + 3i
= 2 + 3i2o) z2 = ?1 ? 4i 
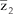 = ?1 + 4i
= ?1 + 4i

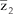 = ?1 + 4i
= ?1 + 4i3o) z3 = ?3i 
 = 3i
= 3i

 = 3i
= 3i4o) z4 = 2 
 = 2
= 2

 = 2
= 2Propriedade

O produto de um número complexo pelo seu conjugado é sempre um número real.

Demonstração

Sendo z = a + bi e 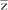 = a ? bi (a
= a ? bi (a  R e b
R e b  R) temos:
R) temos:
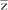 = a ? bi (a
= a ? bi (a  R e b
R e b  R) temos:
R) temos: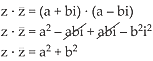

Como a e b são reais, z · 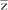
 R.
R.
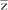
 R.
R.Potência de números complexos
O cálculo de potências de números reais com expoente natural é realizado através de uma multiplicação em que todos os fatores são iguais à base e em quantidade igual ao expoente natural.
Veja que a potência abaixo é o resultado de uma multiplicação com 3 fatores iguais a 5:

Esta outra potência é resultado de uma multiplicação contendo 4 fatores iguais a 7:

No caso de potências de números complexos com expoente natural o procedimento é o mesmo:
Veja que a potência abaixo é o resultado de uma multiplicação com 3 fatores iguais a 5:
Esta outra potência é resultado de uma multiplicação contendo 4 fatores iguais a 7:
No caso de potências de números complexos com expoente natural o procedimento é o mesmo:
Sabemos que:

Por exemplo
Faremos a divisão de 125 por 4:

Calcular o valor de i125 é o mesmo que calcular o valor de i elevado ao resto da divisão de 125 por 4, ou seja, é o mesmo que calcular i1.
Assim,
i125 = i1 = i
Assim,
i125 = i1 = i
exemplo 2:
Aplicando as propriedades da potência, calcule (2 ? 2i)6.
Podemos fatorar o expoente da seguinte forma:
[(2 ? 2i)2]3 =
[22 ? 2 * 2 * (2i) + (2i)2]3
[4 ? 8i + 4i2]3 =
[4 ? 8i + 4 * (?1)]3 =
[4 ? 8i ? 4]3 =
[? 8i]3 =
? 512 * i3 =
? 512 * (? i) =
+ 512i
exemplo 3:
Calcular i359
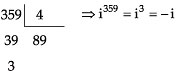
[(2 ? 2i)2]3 =
[22 ? 2 * 2 * (2i) + (2i)2]3
[4 ? 8i + 4i2]3 =
[4 ? 8i + 4 * (?1)]3 =
[4 ? 8i ? 4]3 =
[? 8i]3 =
? 512 * i3 =
? 512 * (? i) =
+ 512i
exemplo 3:
Calcular i359
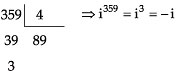
Exercícios números complexos
1) (PUC-MG) Qualo é o quociente de (8 + i)/(2 - i) é igual a
a) 1 + 2i b) 2 + i c) 2 + 2i d) 2 + 3i e) 3 + 2i
2) Sendo z = 5i + 3i2 - 2i3 + 4i27 e w = 2i12 - 3i15 , calcule Im(z).w + Im(w).z .
a) -3 + 18i b) -3 + 10i c) - 5 + 18i d) - 5 + 10 i e) -3 + 12i
3) (Mackenzie-SP) O valor da expressão y = i + i2 + i3 + ... + i1001 é:
a) i² b) i c) i³ d) i² + 1 e) i +1
4) (UCSal) Para que o produto (a + i).(3 - 2i) seja real, a deve ser:
a) 2/3 b) 4/3 c) 3/2 d) 3/4 e) 3/5
5) (FESP/UPE) - Seja z = 1+i , onde i é a unidade imaginária. Podemos afirmar que z8 é igual a:
a) 16 b) 161 c) 32 d) 32i e) 32 + 16i
6) Se o número complexo z = 1-i é uma das raízes da equação x10 + a = 0 , então calcule o valor de a.
a) 16i b) 32i c) 40i d) 48i e) 60i
a) 16 b) 161 c) 32 d) 32i e) 32 + 16i
6) Se o número complexo z = 1-i é uma das raízes da equação x10 + a = 0 , então calcule o valor de a.
a) 16i b) 32i c) 40i d) 48i e) 60i
7) ( UFRGS) (1 + i)15 é igual a:
a) 64(1 + i) b) 128(1 ? i) c) 128(?1 ? i) d) 256(?1 + i) e) 256(1 + i)
a) 64(1 + i) b) 128(1 ? i) c) 128(?1 ? i) d) 256(?1 + i) e) 256(1 + i)
8) Dados os números complexos z1= a + bi e z2 = 1 - ??2i. Como z1.z2 = 15, então z1 + z2 é
11) (UFES) O valor da expressão E = x-1 + x2, para x = 1 - i , é
igual a:
a) 8 b) 4 c) 4+4i d) 6+i e) 8 - ?2i
9) (UCMG-MG) O número complexo z, tal que 5z + 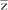 = 12 + 16i, é igual a:
= 12 + 16i, é igual a:
 = 12 + 16i, é igual a:
= 12 + 16i, é igual a:a) ? 2 + 2i b) 2 + 4i c) 2 ? 3i d) 3 + i e) 1 + 2i
10) (FCC-BA) O número complexo 1 ? i é raiz da equação x2 + kx + t = 0 (k, t  R ) se, e somente se:
R ) se, e somente se:
 R ) se, e somente se:
R ) se, e somente se: a) k = t = ? 2 b) k = 2 e t = ? 2 c) k = t = 2 d) k + t = 1 e) k = ?2 e t = 2
a)-3i b)1-i c) 5/2 + (5/2)i d) 5/2 - (3/2)i e) 1/2 - (3/2)i
12) (FUVEST) Sendo i a unidade imaginária (i2 = -1) pergunta-se: quantos números reais a existem para os quais (a + 1)4 é um número real?
a) 1 b) 2 c) 3 d) 4 e) 5
13) (UEFS) Se m - 1 + ni = (3 + i).(1 + 3i), então m e n são respectivamente:
a) 1 e 10 b) 5 e 10 c) 7 e 9 d) 5 e 9 e) 0 e -9
a) -3i b) 1 ? i c) 5/2 + (5/2)i d) 5/2 - (3/2)i e) ½ - (3/2)i
15) (Unitau) O módulo de z=1/i36 é:
a) 3. b) 1. c) 2 d) 1/36. e) 36.
16) O número complexo 2 + i é raiz do polinômio P(x) = x³ + ax² + bx +15, em que a e b são números reais. Pede-se determinar os valores de a e b e, em seguida, calcular P(i) / (3+i) na forma c + di , sendo c e d números reais.
Solução:
a) 1 b) 2 c) 3 d) 4 e) 5
13) (UEFS) Se m - 1 + ni = (3 + i).(1 + 3i), então m e n são respectivamente:
a) 1 e 10 b) 5 e 10 c) 7 e 9 d) 5 e 9 e) 0 e -9
14) (UEFS) O valor da expressão E = x-1 + x2, para x = 1 - i, é:
a) -3i b) 1 ? i c) 5/2 + (5/2)i d) 5/2 - (3/2)i e) ½ - (3/2)i
15) (Unitau) O módulo de z=1/i36 é:
a) 3. b) 1. c) 2 d) 1/36. e) 36.
16) O número complexo 2 + i é raiz do polinômio P(x) = x³ + ax² + bx +15, em que a e b são números reais. Pede-se determinar os valores de a e b e, em seguida, calcular P(i) / (3+i) na forma c + di , sendo c e d números reais.
Solução:
Ora, se x = 2 + i é raiz de P(x), então:
(2 + i)3 + a(2 + i)2 + b(2 + i) + 15 = 0
(2 + i)3 + a(2 + i)2 + b(2 + i) + 15 = 0
Desenvolvendo, vem:
23 + 3.22.i + 3.2.i2 + i3 + a(22 + 2.2.i + i2) + b(2 + i) + 15 = 0
8 + 12i - 6 - i + a(4 + 4i -1) + 2b + bi + 15 = 0
8 + 12i - 6 - i + 4 a + 4ai - a + 2b + bi + 15 = 0
23 + 3.22.i + 3.2.i2 + i3 + a(22 + 2.2.i + i2) + b(2 + i) + 15 = 0
8 + 12i - 6 - i + a(4 + 4i -1) + 2b + bi + 15 = 0
8 + 12i - 6 - i + 4 a + 4ai - a + 2b + bi + 15 = 0
Simplificando e ordenando, vem:
(8 - 6 + 4 a - a + 2b + 15) + (12 - 1 + 4 a + b) i = 0
(17 + 3 a + 2b) + (11 + 4 a + b) i = 0 + 0i
(8 - 6 + 4 a - a + 2b + 15) + (12 - 1 + 4 a + b) i = 0
(17 + 3 a + 2b) + (11 + 4 a + b) i = 0 + 0i
Daí, vem:
17 + 3 a + 2b = 0
11 + 4 a +b = 0
17 + 3 a + 2b = 0
11 + 4 a +b = 0
Ou,
3 a + 2b = - 17
4 a + b = - 11
3 a + 2b = - 17
4 a + b = - 11
Para resolver o sistema de equações acima, multiplicaremos a primeira equação por 4 e a segunda por - 3:
Teremos:
12 a + 8b = - 68
-12 a - 3b = 33
Teremos:
12 a + 8b = - 68
-12 a - 3b = 33
Somando membro a membro - para eliminar a incógnita a - vem:
5b = - 35, de onde conclui-se b = -7.
5b = - 35, de onde conclui-se b = -7.
Portanto, como 4 a + b = - 11, vem, substituindo: 4 a +(-7) = -11, de onde conclui-se:
a = - 1
Logo, a = -1 e b = - 7, responde à primeira parte do exercício.
a = - 1
Logo, a = -1 e b = - 7, responde à primeira parte do exercício.
Portanto, substituindo os valores de a e de b encontrados, o polinômio dado é igual a:
P(x) = x3 - x2 - 7x + 15
Falta calcular P(i) / (3+i).
P(i) = i3 - (i)2 - 7(i) + 15 = -i + 1 -7i + 15 = 16 - 8i
P(x) = x3 - x2 - 7x + 15
Falta calcular P(i) / (3+i).
P(i) = i3 - (i)2 - 7(i) + 15 = -i + 1 -7i + 15 = 16 - 8i
Portanto,
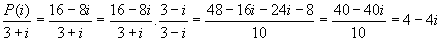
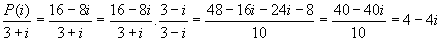
- Polinômios Questões Vestibular
Adição e subtração de polinômios O procedimento utilizado na adição e subtração de polinômios envolve técnicas de redução de termos semelhantes, operações envolvendo sinais iguais e sinais diferentes e jogo de sinal. Observe os exemplos:...
- Múltiplos E Divisores De Um Numero Natural Questões E Teoria
Artigo sobre múltiplos e divisores de um número natural com questões de fixação. Divisor de um número natural Um número é divisor de outro quando o resto da divisão for igual a 0. Portanto, 12 é divisível por 1, 2, 3, 4, 6 e 12. 36 é divisível...
- Números Inteiros Questões
Conjunto dos números inteiros Pertencem ao conjunto dos números inteiros, os números negativos e também o Conjunto dos Números Naturais. Os números positivos são opostos aos números negativos e os negativos opostos aos positivos. Sua...
- Radiciação Propriedades Dos Radicais
Artigo sobre radiciação e as propriedades dos radicais. O tópico em questão agora é a radiciação que é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões...
- Propriedades Das Potências
Artigo sobre potenciação: propriedades das potências, potência fracionária, potência de base 10, potência de base zero, potenciação de números racionais e potenciação de monômios As principais operações são: adição, subtração, divisão...
