Vestibular
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base.
Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos:
logbx = logby, onde x = y
logbx = a, onde x = ba
Exercícios resolvidos
Restrição:
x + 2 > 0
x > ? 2
x + 2 ? 1
x ? 1 ? 2
x ? ? 1
2x² + x > 0
x*(2x + 1) > 0
x > 0
2x + 1 > 0
2x > ? 1
x > ?1/2
Resolução:
log x + 2 (2x² + x) = 1
2x² + x = (x + 2)¹
2x² + x = x + 2
2x² + x ? x ? 2 = 0
2x² ? 2 = 0
2x² = 2
x² = 2/2
x² = 1
?x² = ?1
x? = ? 1
x?? = 1
De acordo com as restrições entre os resultados x? = 1 e x?? = ?1, temos que considerar somente x = 1, de forma a tornar o conjunto solução verdadeiro.
- Exercícios Função Exponencial
1) (PUCRS) Se , então x pertence ao intervalo (A) [0; 1) (B) (0; 2) (C) (1; 2) (D) (1; 3) (E) (2; 3)- Neste exercícios podemos dizer que a potência da esquerda tem "4 níveis". Temos que ir "cortando" um a um. Vamos igualar a primeira...
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Equações Logaritmicas Questões Vestibular
Agora exercícios sobre equações logarítmicas com gabarito para você praticar e se dá bem no vestibular. mãos a obra ;D 1) A equação tem duas raízes reais. O produto dessas raízes é: a) ...
- Inequações Logarítmicas Exercícios E Exemplos
Ao estudarmos as inequações logarítmicas, devemos ter cuidados especiais com as restrições a que devem estar submetidas a incógnita. Para resolvê-las, procuraremos obter nos dois membros logaritmos de mesma base. A partir disso, trabalharemos...
Vestibular
Equações Logarítmicas: aprenda como resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base.
Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos:
logbx = a, onde x = ba
Exercícios resolvidos
1) log2x + log2 (x ? 2) = log228
Restrição:
x > 0
x ? 2 > 0
x > 2
Restrição:
x > 0
x ? 2 > 0
x > 2
log2x + log2 (x ? 2) = log228
log2 x * (x ? 2) = log228
x * (x ? 2) = 8
x² ? 2x ? 8 = 0
Aplicando o Teorema de Bháskara
? = 36
x? = 4
x?? = ? 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
log2 x * (x ? 2) = log228
x * (x ? 2) = 8
x² ? 2x ? 8 = 0
Aplicando o Teorema de Bháskara
? = 36
x? = 4
x?? = ? 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
2) log4(x ? 3) = log4(? x + 7)
restrição:
x - 3 > 0
x = > 3
- x + 7 > 0
- x > - 7 * ( - 1)
x > 7
x ? 3 = ? x + 7
x + x = 7 + 3
2x = 10
x = 10/2
x = 5
x + x = 7 + 3
2x = 10
x = 10/2
x = 5
3) 
Neste caso temos a seguinte condição de existência:
Voltando à equação temos:
Aplicando a mesma propriedade que aplicamos nos casos anteriores e desenvolvendo os cálculos temos:
Como 25 satisfaz a condição de existência, então S = {25} é o conjunto solução da equação.
Se quisermos recorrer a outras propriedades dos logaritmos também podemos resolver este exercício assim:
Lembre-se que e que log5 625 = 4, pois 54 = 625.
4) Encontre a solução da equação
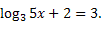
Solução: Pela definição de logaritmo temos:
5x + 2 = 33
5x + 2 = 27
5x = 27 ? 2
5x = 25
x = 5
Portanto S = {5}.
5) Resolva a seguinte equação:
Solução:
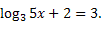
Solução: Pela definição de logaritmo temos:
5x + 2 = 33
5x + 2 = 27
5x = 27 ? 2
5x = 25
x = 5
Portanto S = {5}.
5) Resolva a seguinte equação:
 |
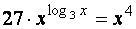Solução:
Novamente um problema que parece ser extraordinário, mas que um pouco de planejamento se torna banal:
O segredo deve estar em "remover" o exponencial em logaritmo na base 3. Pela fórmula (I) talvez alguma coisa possa ser feita. Se o primeiro membro inteiro fosse um logaritmo, o exponencial poderia "sair". Ora deve-se então transformar o primeiro membro em um logaritmo e de preferência na base 3 e para fazer isso o segundo membro deve ser transformado em um log:
Segundo a fórmula de multiplicação:
Como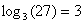
e e usando-se (I) nos 2 outros elementos:
Veja que já se ilumina o fim do túnel, substituindo por y o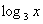
:
Cujas soluções são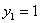
e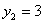 
substituindo por :
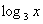e
6) Resolver a equação logarítmica log2x + log2 (x ? 2) = log228
Restrição:
x > 0
x ? 2 > 0
x > 2
log2x + log2 (x ? 2) = log228
log2 x * (x ? 2) = log228
x * (x ? 2) = 8
x² ? 2x ? 8 = 0
Aplicando Bháskara
? = 36
x? = 4
x?? = ? 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
O segredo deve estar em "remover" o exponencial em logaritmo na base 3. Pela fórmula (I) talvez alguma coisa possa ser feita. Se o primeiro membro inteiro fosse um logaritmo, o exponencial poderia "sair". Ora deve-se então transformar o primeiro membro em um logaritmo e de preferência na base 3 e para fazer isso o segundo membro deve ser transformado em um log:
 |
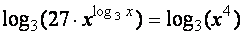Segundo a fórmula de multiplicação:
 |
 |
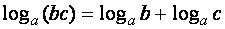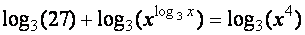Como
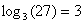e e usando-se (I) nos 2 outros elementos: |
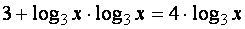Veja que já se ilumina o fim do túnel, substituindo por y o
: |
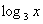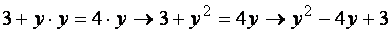Cujas soluções são
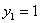e 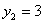substituindo por : |
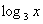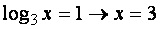e
 |
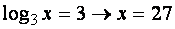Restrição:
x > 0
x ? 2 > 0
x > 2
log2x + log2 (x ? 2) = log228
log2 x * (x ? 2) = log228
x * (x ? 2) = 8
x² ? 2x ? 8 = 0
Aplicando Bháskara
? = 36
x? = 4
x?? = ? 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
7) Resolva a equação logarítmica log x + 2 (2x² + x) = 1
Restrição:
x + 2 > 0
x > ? 2
x + 2 ? 1
x ? 1 ? 2
x ? ? 1
2x² + x > 0
x*(2x + 1) > 0
x > 0
2x + 1 > 0
2x > ? 1
x > ?1/2
Resolução:
log x + 2 (2x² + x) = 1
2x² + x = (x + 2)¹
2x² + x = x + 2
2x² + x ? x ? 2 = 0
2x² ? 2 = 0
2x² = 2
x² = 2/2
x² = 1
?x² = ?1
x? = ? 1
x?? = 1
De acordo com as restrições entre os resultados x? = 1 e x?? = ?1, temos que considerar somente x = 1, de forma a tornar o conjunto solução verdadeiro.
- Exercícios Função Exponencial
1) (PUCRS) Se , então x pertence ao intervalo (A) [0; 1) (B) (0; 2) (C) (1; 2) (D) (1; 3) (E) (2; 3)- Neste exercícios podemos dizer que a potência da esquerda tem "4 níveis". Temos que ir "cortando" um a um. Vamos igualar a primeira...
- Equação Geral E Reduzida Da Reta - Resumo (com Questões)
Equação geral da reta Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos...
- Sistema De Inequação Do 1º Grau Exercícios
Sistema de inequação do 1º grau Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas. Quando terminamos a...
- Equações Logaritmicas Questões Vestibular
Agora exercícios sobre equações logarítmicas com gabarito para você praticar e se dá bem no vestibular. mãos a obra ;D 1) A equação tem duas raízes reais. O produto dessas raízes é: a) ...
- Inequações Logarítmicas Exercícios E Exemplos
Ao estudarmos as inequações logarítmicas, devemos ter cuidados especiais com as restrições a que devem estar submetidas a incógnita. Para resolvê-las, procuraremos obter nos dois membros logaritmos de mesma base. A partir disso, trabalharemos...