Vestibular

Inequações logarítmicas exercícios e exemplos

Ao estudarmos as inequações logarítmicas, devemos ter cuidados especiais com as restrições a que devem estar submetidas a incógnita. Para resolvê-las, procuraremos obter nos dois membros logaritmos de mesma base. A partir disso, trabalharemos apenas com os logaritmandos, usando o fato de a função ser crescente ou decrescente:

a) mantendo para eles o mesmo sinal da inequação quando a base for maior que 1, pois a função é crescente;

b) invertendo para eles o sinal da inequação quando a base estiver entre 0 e 1, pois a função é decrescente.

Ex: Resolver a inequação log2 x - 1 > 5.

Temos que ? log2 x - 1 > 5*log2 2 ? log2 x - 1 > log2 25 ? log2 x - 1 > log2 32

Como a base é 2 > 1, a função logarítmica é crescente e, portanto, o sinal > da inequação deve ser mantido para os logaritmandos, ou seja, devemos ter x ? 1 > 32.

Então, x > 32 + 1 ? x > 33 ( I )

A solução é o conjunto dos valores de x que, além de tornar ( I ) verdadeiro, satisfazem também a restrição inicial.

Desse modo, a restrição deverá ser ? mais trabalhada?, ou seja: x ? 1 > 0 ? x > 1 ( II )

O conjunto solução é S = {x ? R/x > 33}.

Ex2: O número real x que satisfaz a equação log₂(12 ? 2^x) = 2x é:

Solução:

log₂(12 ? 2^x) = 2x

12 ? 2 = 2^2x

2^2x + 2x ? 12 = 0

(2^x)² + 2^x ? 12 = 0

Substituindo 2^x por y, temos:

y² + y ? 12 = 0

Resolvendo a equação do 2.º grau acima, temos:

y? = -4 ; y?? = 3

2^x= -4

2^x = 3 x = log₂3

Exercícios inequações logarítmicas

1) Resolva a inequação log3 (2 ? 5x) ? log3 3

2) Resolva a inequação logarítmica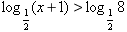

3) Determine para quais valores de x o número logx+1 (2 - x) está definido nos reais

4) (Unicamp) Suponha que o preço de um automóvel tenha uma desvalorização de 19% ao ano sobre o preço do ano anterior. Se F representa o preço inicial (preço de fábrica) e p(t) o preço após t anos, pede-se:

a) A expressão para p(t)

b) O tempo mínimo necessário, em número inteiro de anos, após a saída da fábrica, para que um automóvel venha a valer menos que 5% do valor inicial. Se necessário, use:

log2 = 0,301 log3 = 0,477

5) (Fuvest) Seja f(x) o logaritmo de 2x na base

.

Resolva a inequação f(x) > 1.

Gabarito:

1) S = { x ? R/ -1/5 ? x < 2/5} 2) 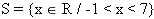3) S = { x ? R/ -1 < x < 2 e x ? 0}

4) a) p(t) = (0,81)t F b) t = 15 anos 5) S= {x $\in$ R | 0 < x < $1 - \frac{\sqrt{2}}{2}$ ou $\frac{\sqrt{2}}{2}$ < x < $1 + \frac{\sqrt{2}}{2}$ }

- Exercícios Função Exponencial
1) (PUCRS) Se , então x pertence ao intervalo (A) [0; 1) (B) (0; 2) (C) (1; 2) (D) (1; 3) (E) (2; 3)- Neste exercícios podemos dizer que a potência da esquerda tem "4 níveis". Temos que ir "cortando" um a um. Vamos igualar a primeira...

- Propriedades Dos Logaritmos Com Exemplos
É fácil demonstrar as seguintes propriedades dos logaritmos, todas decorrentes da definição: O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma: logab = x ? ax =...

- Inequações 2º Grau Exercícios Resolvidos Vestibular
São expressões matemáticas que apresentam os sinais de maior (>) , maior ou igual (? ), menor (< ), menor ou igual (? ) e diferente (?) ao invés do sinal de igualdade que caracteriza as equações. Devem ser resolvidas usando a fórmula de Bháskara e...

- Equações Logaritmicas Questões Vestibular
Agora exercícios sobre equações logarítmicas com gabarito para você praticar e se dá bem no vestibular. mãos a obra ;D 1) A equação tem duas raízes reais. O produto dessas raízes é: a) ...

- Equações Logarítmicas: Aprenda Como Resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base. Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos: logbx = logby, onde x = y logbx...

Vestibular