Vestibular
São expressões matemáticas que apresentam os sinais de maior (>) , maior ou igual (? ), menor (< ), menor ou igual (? ) e diferente (?) ao invés do sinal de igualdade que caracteriza as equações. Devem ser resolvidas usando a fórmula de Bháskara e comparando o resultado com o sinal da inequação, formulando assim, o resultado da inequação.
Veja alguns exemplos resolvidos para melhor compreensão:
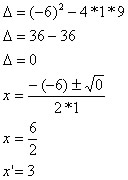
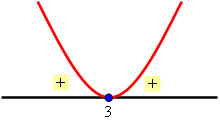 S = {x ? R / x <> 3}
S = {x ? R / x <> 3}
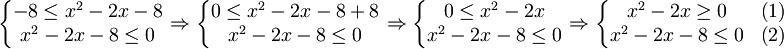
Resolvendo (2):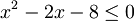 , obtemos que:
, obtemos que: 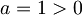 ;
; 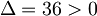 ;
; 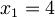 e
e 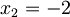 .
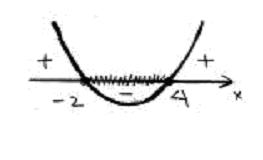
.
Resolvendo (1):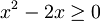 , obtemos que:
, obtemos que: 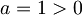 ;
; 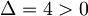 ;
; 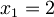 e
e 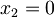 .
.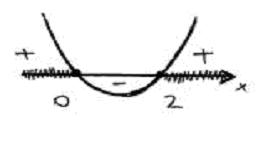
Como temos duas soluções que devem ser satisfeitas simultâneamente, vamos calcular a intersecção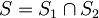 :
: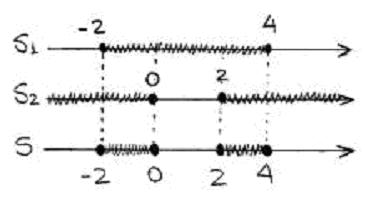
Portanto,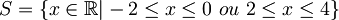 .
.
- Exercícios Função Exponencial
1) (PUCRS) Se , então x pertence ao intervalo (A) [0; 1) (B) (0; 2) (C) (1; 2) (D) (1; 3) (E) (2; 3)- Neste exercícios podemos dizer que a potência da esquerda tem "4 níveis". Temos que ir "cortando" um a um. Vamos igualar a primeira...
- área Do Quadrado Questões Vestibular
Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S= 36 cm Quando dispomos da medida das diagonais do quadrado,...
- área Do Quadrado Questões Vestibular
Artigo sobre área do quadrado com questões de fixação. Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S=...
- Equações Logarítmicas: Aprenda Como Resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base. Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos: logbx = logby, onde x = y logbx...
- Inequações Logarítmicas Exercícios E Exemplos
Ao estudarmos as inequações logarítmicas, devemos ter cuidados especiais com as restrições a que devem estar submetidas a incógnita. Para resolvê-las, procuraremos obter nos dois membros logaritmos de mesma base. A partir disso, trabalharemos...
Vestibular
Inequações 2º grau exercícios resolvidos vestibular
São expressões matemáticas que apresentam os sinais de maior (>) , maior ou igual (? ), menor (< ), menor ou igual (? ) e diferente (?) ao invés do sinal de igualdade que caracteriza as equações. Devem ser resolvidas usando a fórmula de Bháskara e comparando o resultado com o sinal da inequação, formulando assim, o resultado da inequação.
Veja alguns exemplos resolvidos para melhor compreensão:
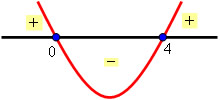
Ex1: Determine a solução da inequação x² ? 4x ? 0.
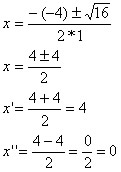
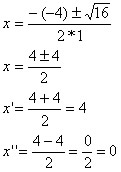

Ex2: Calcule a solução da inequação x² ? 6x + 9 > 0.
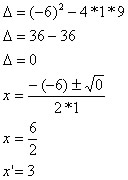

Ex3: 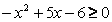
Achando as raízes da função, temos
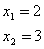
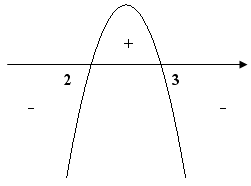
E o estudo do sinal (a função é côncava para baixo, pois a < 0):
A solução é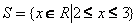 .
.
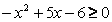
Achando as raízes da função, temos
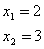
E o estudo do sinal (a função é côncava para baixo, pois a < 0):

A solução é
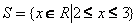 .
.Exercício resolvido
Resolver a seguinte inequação: 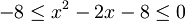 .
.
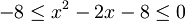 .
.Então, queremos que: 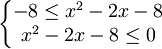
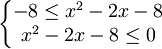
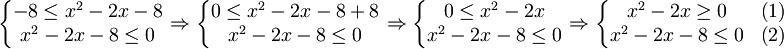
Resolvendo (2):
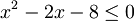 , obtemos que:
, obtemos que: 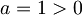 ;
; 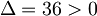 ;
; 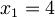 e
e 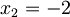 .
.
Resolvendo (1):
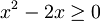 , obtemos que:
, obtemos que: 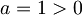 ;
; 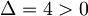 ;
; 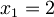 e
e 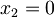 .
.
Como temos duas soluções que devem ser satisfeitas simultâneamente, vamos calcular a intersecção
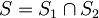 :
:
Portanto,
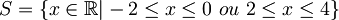 .
.- Exercícios Função Exponencial
1) (PUCRS) Se , então x pertence ao intervalo (A) [0; 1) (B) (0; 2) (C) (1; 2) (D) (1; 3) (E) (2; 3)- Neste exercícios podemos dizer que a potência da esquerda tem "4 níveis". Temos que ir "cortando" um a um. Vamos igualar a primeira...
- área Do Quadrado Questões Vestibular
Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S= 36 cm Quando dispomos da medida das diagonais do quadrado,...
- área Do Quadrado Questões Vestibular
Artigo sobre área do quadrado com questões de fixação. Para calcular a área de um quadrado, basta elevar ao quadrado a medida de um lado, ou seja, S = L²Exemplo: O lado de um quadrado mede 6 cm. calcule sua área.S = L²S= 6²S=...
- Equações Logarítmicas: Aprenda Como Resolver
São equações que apresentam logaritmos com a incógnita figurando no logaritmo, no logaritmando ou na base. Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos: logbx = logby, onde x = y logbx...
- Inequações Logarítmicas Exercícios E Exemplos
Ao estudarmos as inequações logarítmicas, devemos ter cuidados especiais com as restrições a que devem estar submetidas a incógnita. Para resolvê-las, procuraremos obter nos dois membros logaritmos de mesma base. A partir disso, trabalharemos...
