Vestibular
Na geometria, as ideias de ponto, reta e plano são consideradas como conceitos primitivos, ou seja, sabemos o que cada uma significa, mas não as definimos. Habitualmente, usamos a seguinte notação:
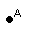
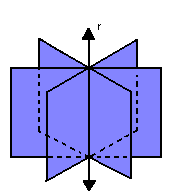
. Duas retas no espaço podem possuir 3 posições relativas:
Retas concorrentes: duas retas são concorrentes se, e somente se, possuírem um ponto em comum:
Retas paralelas: duas retas são paralelas se, e somente se, forem coplanares e não possuírem ponto em comum:
Obs.: um caso particular de paralelismo ocorre se as retas forem coincidentes (r ? s).
Retas reversas: duas retas são reversas se, e somente se, não forem coplanares e não possuírem ponto em comum:
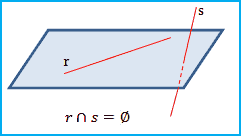
Obs.: se houver um plano que contenha a reta r e que forme um ângulo de 90o com a reta s, as retas serão reversas e ortogonais.
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- Posições Relativas
As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. Dentre as posições relativas, podemos destacar: Posições relativas de duas retas Duas retas no espaço podem possuir 3 posições relativas: Retas...
- Determinação De Um Plano
Determinação de um plano É possível determinar um plano de quatro maneiras. Vejamos: 1º caso: Três pontos não-colineares determinam um ponto. Se A, B e C são pontos não-colineares, então... existe só um plano tal que: A ? , B ? ...
- Segmento De Reta E Semirreta Geometria Plana
Tentarei explicar neste artigo sobre segmeto de reta e semirreta assunto importante na Geometria plana. Segmento de reta Se considerarmos uma reta r e sobre ela marcarmos dois pontos, A e B, distintos, o conjunto de pontos formado pelo ponto A, e pelo...
- Tipos De Retas - Geometria
Vejamos agora alguns tipos de retas A reta é um elemento geométrico de comprimento infinito, com apenas uma dimensão. Veja nos agora, alguns tipos de retas: Retas Paralelas Duas retas são paralelas quando são equidistantes durante toda...
Vestibular
axiomas de Euclides
Na geometria, as ideias de ponto, reta e plano são consideradas como conceitos primitivos, ou seja, sabemos o que cada uma significa, mas não as definimos. Habitualmente, usamos a seguinte notação:
- pontos: letras maiúsculas do nosso alfabeto
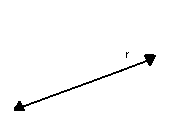
- retas: letras minúsculas do nosso alfabeto

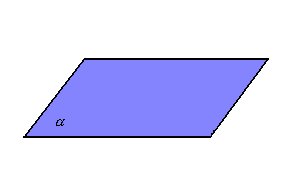
- planos: letras minúsculas do alfabeto grego

Observação: Espaço é o conjunto de todos os pontos.
Por exemplo, da figura a seguir, podemos escrever:
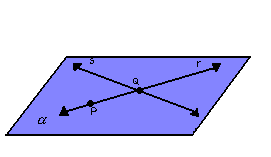 | 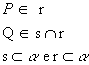 |
Axiomas
Axiomas, ou postulados (P), são proposições aceitas como verdadeiras sem demonstração e que servem de base para o desenvolvimento de uma teoria.
Temos como axioma fundamental:existem infinitos pontos, retas e planos.
P1) Por um único ponto passam infinitas retas.


P2) Por dois pontos distintos A e B passa uma única reta.

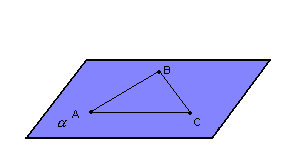
P3) Para determinarmos um plano necessitamos de pelo menos três pontos.

P4) Se dois pontos distintos de uma reta pertencem a um plano, então todos os pontos dessa reta pertencem ao plano.

P5) Existem infinitos pontos dentro e fora de um plano


P3) Para determinarmos um plano necessitamos de pelo menos três pontos.

P4) Se dois pontos distintos de uma reta pertencem a um plano, então todos os pontos dessa reta pertencem ao plano.

P5) Existem infinitos pontos dentro e fora de um plano

Postulados sobre o plano e o espaço
P6) Por três pontos não-colineares passa um único plano.

P7) O plano é infinito, isto é, ilimitado.
P8) Por uma reta pode ser traçada uma infinidade de planos.

P9) Toda reta pertencente a um plano divide-o em duas regiões chamadas semiplanos.
P10) Qualquer plano divide o espaço em duas regiões chamadas semi-espaços.
Posições relativas de duas retas
. Duas retas no espaço podem possuir 3 posições relativas:
Retas concorrentes: duas retas são concorrentes se, e somente se, possuírem um ponto em comum:
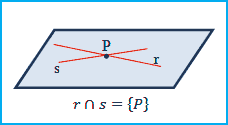 |
Retas paralelas: duas retas são paralelas se, e somente se, forem coplanares e não possuírem ponto em comum:
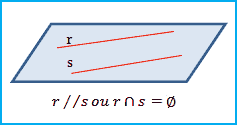 |
Obs.: um caso particular de paralelismo ocorre se as retas forem coincidentes (r ? s).
Retas reversas: duas retas são reversas se, e somente se, não forem coplanares e não possuírem ponto em comum:

Obs.: se houver um plano que contenha a reta r e que forme um ângulo de 90o com a reta s, as retas serão reversas e ortogonais.
Postulados de Euclides
Duas coisas iguais somadas com uma terceira são iguais entre si.
Se adicionarmos parcelas iguais a quantidades iguais, as somas continuarão iguais.
Se as mesmas quantidades forem subtraídas de quantidades iguais, os restos continuarão a ser iguais.
Situações que se coincidem são iguais umas com as outras.
O todo é maior que as partes.
Duas coisas iguais somadas com uma terceira são iguais entre si.
Se adicionarmos parcelas iguais a quantidades iguais, as somas continuarão iguais.
Se as mesmas quantidades forem subtraídas de quantidades iguais, os restos continuarão a ser iguais.
Situações que se coincidem são iguais umas com as outras.
O todo é maior que as partes.
- Distância Entre Ponto E Reta Questões Vestibular
Artigo sobre distância entre ponto e reta com questões de vestibulares resolvidas. Distância entre ponto e reta Vamos realizar o estudo analítico da distância entre um ponto e uma reta no plano cartesiano. Considere um ponto P(xo, yo) e uma reta...
- Posições Relativas
As figuras planas e espaciais são formadas pela intersecção de retas e planos pertencentes ao espaço. Dentre as posições relativas, podemos destacar: Posições relativas de duas retas Duas retas no espaço podem possuir 3 posições relativas: Retas...
- Determinação De Um Plano
Determinação de um plano É possível determinar um plano de quatro maneiras. Vejamos: 1º caso: Três pontos não-colineares determinam um ponto. Se A, B e C são pontos não-colineares, então... existe só um plano tal que: A ? , B ? ...
- Segmento De Reta E Semirreta Geometria Plana
Tentarei explicar neste artigo sobre segmeto de reta e semirreta assunto importante na Geometria plana. Segmento de reta Se considerarmos uma reta r e sobre ela marcarmos dois pontos, A e B, distintos, o conjunto de pontos formado pelo ponto A, e pelo...
- Tipos De Retas - Geometria
Vejamos agora alguns tipos de retas A reta é um elemento geométrico de comprimento infinito, com apenas uma dimensão. Veja nos agora, alguns tipos de retas: Retas Paralelas Duas retas são paralelas quando são equidistantes durante toda...
