Vestibular
Artigo sobre ângulos opostos com questões resolvidas para fixação do conteúdo
Consideramos ângulos opostos pelo vértice, aqueles que possuem um lado como sendo semirretas opostas aos lados dos outros.
Note que duas retas concorrentes determinam dois pares de ângulos opostos pelo vértice.
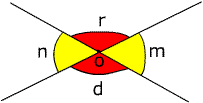
O é o vértice dos ângulos m, n, r e d
Analisando a figura notamos que, m e n são ângulos opostos pelo vértice, o mesmo acontece com os ângulos r e d.
Os ângulos opostos pelo vértice são ângulos congruentes (iguais).
Logo:
m = n e r = d
Observamos também que:
m + r = 180º, m + d = 180º, n + r = 180º, n + d = 180º
questões resolvidas ângulos opostos ao vértice
1) Observe a figura abaixo e determine o valor de m e n.
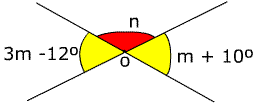
3m - 12º e m + 10º, são ângulos opostos pelo vértice logo são iguais.
3m - 12º = m + 10º
3m - m = 10º + 12º
2m = 22º
m = 22º/2
m = 11º
m + 10º e n, são ângulos suplementares logo a soma entre eles é igual a 180º.
(m + 10º) + n = 180º
(11º + 10º) + n = 180º
21º + n = 180º
n = 180º - 21º
n = 159º
Resposta: m = 11º e n = 159º
2) Dois ângulos opostos pelo vértice têm medidas, em graus, expressas por x + 60º e 3x - 40º. Qual é o valor de x?
Solução:
4) Na figura, a medida dos dois ângulos assinalados é
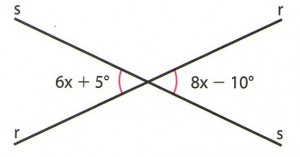
a) 50º b) 40º c) 30º d) 60º e) 70º
5) A medida do ângulo x é:
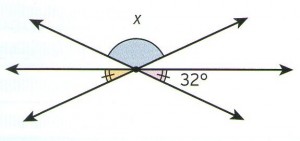
a) 232º b) 32º c) 116º d) 64º e) 100º
6) O valor de x é
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
- ângulos Congruentes, Consecutivos E Adjacentes.
Estudaremos agora ângulos congruentes, consecutivos e adjacentes. Ângulos congruentes Dois ângulos são congruentes quando têm a mesma medida. Observe os ângulos abaixo: Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos...
- ângulos Complementares E Suplementares Questões Resolvidas
COMPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 90º e neste caso, um ângulo é o complemento do outro. Ex.: 30o e 50o (30+50=90) ou37o e 53o (37+53=90) ou20o e 70o (20+70=90) ... SUPLEMENTARES:...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
- ângulos Definição E Classificação
Esse artigo aborda definição, bissetriz e classificação dos ângulos. ÂNGULO: É uma figura aberta cujos lados se prolongam indefinidamente num sentido. Os lados do ângulo são semirretas com a mesma origem, chamando-se a esta origem vértice....
Vestibular
ângulos opostos pelo vértice exercícios resolvidos
Artigo sobre ângulos opostos com questões resolvidas para fixação do conteúdo
Consideramos ângulos opostos pelo vértice, aqueles que possuem um lado como sendo semirretas opostas aos lados dos outros.
Note que duas retas concorrentes determinam dois pares de ângulos opostos pelo vértice.

O é o vértice dos ângulos m, n, r e d
Analisando a figura notamos que, m e n são ângulos opostos pelo vértice, o mesmo acontece com os ângulos r e d.
Os ângulos opostos pelo vértice são ângulos congruentes (iguais).
Logo:
m = n e r = d
Observamos também que:
m + r = 180º, m + d = 180º, n + r = 180º, n + d = 180º
questões resolvidas ângulos opostos ao vértice
1) Observe a figura abaixo e determine o valor de m e n.

3m - 12º e m + 10º, são ângulos opostos pelo vértice logo são iguais.
3m - 12º = m + 10º
3m - m = 10º + 12º
2m = 22º
m = 22º/2
m = 11º
m + 10º e n, são ângulos suplementares logo a soma entre eles é igual a 180º.
(m + 10º) + n = 180º
(11º + 10º) + n = 180º
21º + n = 180º
n = 180º - 21º
n = 159º
Resposta: m = 11º e n = 159º
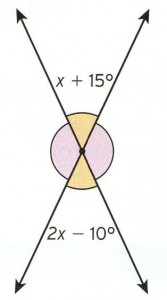
2) Dois ângulos opostos pelo vértice têm medidas, em graus, expressas por x + 60º e 3x - 40º. Qual é o valor de x?
Solução:
x + 60º = 3x - 40º  ângulos o.p.v ângulos o.p.v x - 3x = - 40º - 60º -2x = - 100º x = 50º Logo, o valor de x é 50º. | 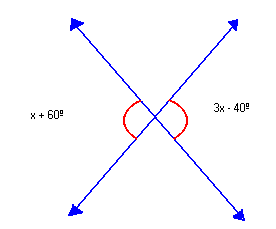 |
3) Dois ângulos opostos pelo vértice medem, em graus, (3x+ 10) e (x + 50). Um deles mede, em graus:
a) 20°
b) 30°
c) 50°
d) 70°
e) 80°
Solução:
Como os ângulos são opostos pelo vértice, então eles são congruentes. Assim temos:
3x + 10 = x + 50
3x ? x = 50 ? 10
2x = 40
x = 40 / 2
x = 20
Note que determinamos o valor de x e não o que está sendo pedido pela questão. Como queremos o valor de um deles, basta substituir o valor de x em qualquer uma das expressões dos ângulos.
Desta forma, x + 50 = 20 + 50 = 70. Logo, a medida de um deles (os dois tem a mesma medida, pois são o.p.v.) é 70°. Portanto, letra D.
4) Na figura, a medida dos dois ângulos assinalados é

a) 50º b) 40º c) 30º d) 60º e) 70º
5) A medida do ângulo x é:

a) 232º b) 32º c) 116º d) 64º e) 100º
6) O valor de x é

a) 40º b) 25º c) 50º d) 70º e) 80º
7) Dois ângulos opostos pelo vértice (OPV) são:
a) complementares
b) congruentes
c) rasos
d) suplementares
8) Dois ângulos opostos pelo vértice medem 105° e 5x - 45°. A medida de x é
a) 30º b) 105º c) 60º d) 90º e) 120º
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
- ângulos Congruentes, Consecutivos E Adjacentes.
Estudaremos agora ângulos congruentes, consecutivos e adjacentes. Ângulos congruentes Dois ângulos são congruentes quando têm a mesma medida. Observe os ângulos abaixo: Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos...
- ângulos Complementares E Suplementares Questões Resolvidas
COMPLEMENTARES: são ângulos na qual a soma de suas medidas é igual a 90º e neste caso, um ângulo é o complemento do outro. Ex.: 30o e 50o (30+50=90) ou37o e 53o (37+53=90) ou20o e 70o (20+70=90) ... SUPLEMENTARES:...
- ângulos No Círculo Com Exemplos Resolvidos
Artigo sobre ângulos no círculo com exemplos resolvidos para um melhor aprendizado. Elementos de um círculo ou circunferência Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura: segmento de reta...
- ângulos Definição E Classificação
Esse artigo aborda definição, bissetriz e classificação dos ângulos. ÂNGULO: É uma figura aberta cujos lados se prolongam indefinidamente num sentido. Os lados do ângulo são semirretas com a mesma origem, chamando-se a esta origem vértice....
