Vestibular

Características do tetraedro
Número de faces: 4.
Número de vértices: 4.
Número de arestas: 6.
Apótema e altura de um tetraedro regular
O Apótema lateral(g) de um tetraedro regular é dado pela fórmula:
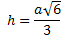
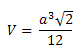
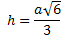 , onde a = 9 cm
, onde a = 9 cm
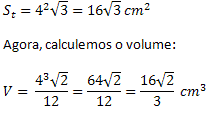
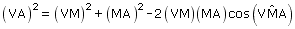
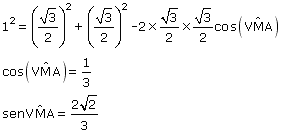
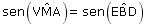
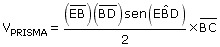
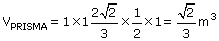
- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- Pirâmides Questões Vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos. Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- Poliedros Convexos E Regulares
Elas representam sólidos, e são exemplos de poliedros De um modo geral, chamamos de Poliedro à região do espaço limitada por polígonos planos, e tais que cada uma das arestas desses...
- Diedros Questões Vestibular
Diedros Dois semiplanos não-coplanares, com origem numa mesma reta, determinam uma figura geométrica chamada ângulo diédrico, ou simplesmente diedro: Secção reta de um diedro Chamamos de seção...
Vestibular
Tetraedros regulares questões
Artigo sobre tetraedros, área e volume dos tetraedros com questões resolvidas e propostas.
O tetraedro regular é um sólido platônico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros (triângulos que possuem lados com medidas iguais); possui 4 vértices , 4 faces e 6 arestas.
Um tetraedro regular é um poliedro regular formado por 4 triângulos equiláteros iguais.

Características do tetraedro
Número de faces: 4.
Número de vértices: 4.
Número de arestas: 6.
Apótema e altura de um tetraedro regular
g = a / 2
/ 2
 / 2
/ 2A altura de um tetraedro regular de aresta a, é dada por:
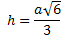
Área total e área lateral de um tetraedro regular
A área total de um tetraedro regular é igual a 4 vezes a área de uma face. Sendo a face um triângulo equilátero de lado a, temos:
Aface = a²?3 / 4
Então a área total de um tetraedro regular de aresta a é dada por:
At = 4 * Aface = 4 * a²?3 / 4
At = a2

A área lateral do tetraedro regular é igual a três vezes a área de uma face. A quarta face corresponde à base da pirâmide.
Então a área lateral é:
Al = 3 * a²?3 / 4
Volume do tetraedro regular
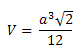
Questões tetraedros regulares
1) A aresta de um tetraedro regular mede 9 cm. calcule a medida da altura, do apótema, a área lateral e área total desse tetraedro.
Solução:
Cálculo da altura:
A medida da altura é dada por:
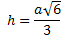 , onde a = 9 cm
, onde a = 9 cmPortanto:
h = 9?3 / 3
h = 3?3 cm.
A altura mede 3?3 cm.
Cálculo do apótema:
A medida do apótema é dada por
g = a / 2, com a = 9 cm.
/ 2, com a = 9 cm.
 / 2, com a = 9 cm.
/ 2, com a = 9 cm.Portanto:
g = a / 2 ? g = 4,5?3 cm.
/ 2 ? g = 4,5?3 cm.
 / 2 ? g = 4,5?3 cm.
/ 2 ? g = 4,5?3 cm.O apótema mede 4,5?3 cm.
Cálculo da área lateral
A área lateral é dada por
Al = 3 * a²?3 / 4 = 3 * 81?3 / 4 = 60,75?3
A área lateral é 60,75?3 cm.
2) Calcule a área total e o volume de um tetraedro regular de 4 cm de aresta.
Solução:
primeiro vamos calcular a área total.
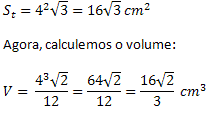
3) (FUVEST-2012) Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a:
a) a?3 b) a?2 c) a?3 / 2 d) a?2 / 2 e) a?2 / 4
Solução:
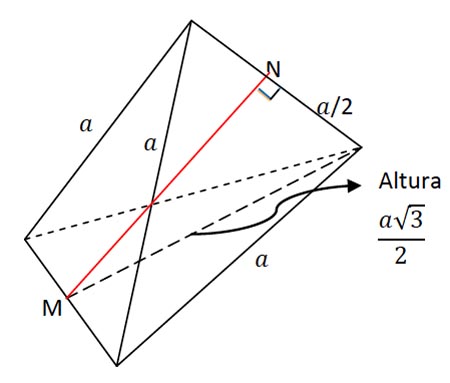
Considerando o seguinte tetraedro regular de lado :

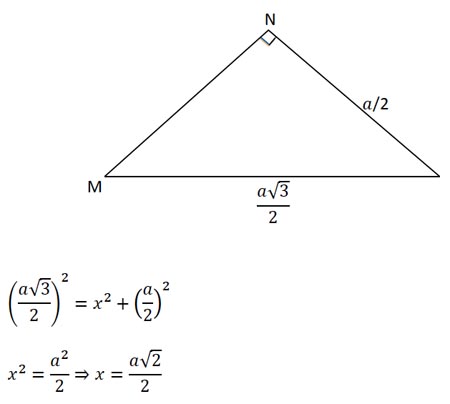
Como a distância entre 2 arestas não adjacentes (reversas) é a medida do segmento perpendicular a ambas (no caso MN). Podemos considerar o triângulo abaixo:

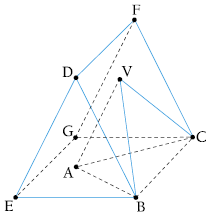
4) (UFRJ) Um artesão retirou, de uma pedra com a forma inicial de um prisma triangular reto de base EBD, um tetraedro regular VABC. Observe a figura abaixo:
Considere os seguintes dados:
? os vértices A e V pertencem a duas faces laterais do prisma;
?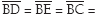 1 m.
1 m.
Determine o volume inicial da pedra.
? os vértices A e V pertencem a duas faces laterais do prisma;
?
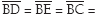 1 m.
1 m.Determine o volume inicial da pedra.
Solução:
De acordo com a figura, as faces VBC e ABC do tetraedro regular encontram-se inscritas nas faces laterais BCFD e BCGE, respectivamente. Então, o ângulo DBE é congruente ao ângulo da seção meridiana VMA que contém o ponto M, médio de BC. Aplicando a lei dos cossenos a esse triângulo, obtém-se:
Substituindo os valores numéricos e resolvendo a equação resultante tem-se:
Como os ângulos VMA e EBD são congruentes, conclui-se que:
Calculando o volume do prisma:
5) A área total de um tetraedro regular é 1296?3 cm². Determine sua altura.
Solução:
A área total é dada por a2 , onde a é a medida da aresta.
, onde a é a medida da aresta.
 , onde a é a medida da aresta.
, onde a é a medida da aresta.Então temos:
a2 = 1296?3 ? a² = 1296 ? a = 36
= 1296?3 ? a² = 1296 ? a = 36
 = 1296?3 ? a² = 1296 ? a = 36
= 1296?3 ? a² = 1296 ? a = 36Assim sendo, a aresta mede 36 cm.
Como a altura é dada por 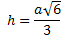 , temos:
, temos:
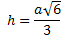 , temos:
, temos:h = 36?6 / 3 ? h = 12?6 cm
A alturas mede 12?6 cm.
6) (SJRP - JUNDIAÍ) Os vértices de um tetraedro regular de volume 1m³ são centros das faces de outro tetraedro regular. O volume deste outro tetraedro vale:
a) 1 m³ b) 3m³ c) 9m³ d) 27m³ e) 81m³
7) Se a área de um tetraedro é regular é 48?3 m², qual a sua área total?
8) (LONDRINA) O tetraedro regular ABCD tem centro O. O ângulo diedro de faces OAB e OAC mede:
a) 30° b) 60° c) 120° d) 135° e) 150°
Gabarito:
6) D 7) 64?3 m² 8) D
- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- Pirâmides Questões Vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos. Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- Poliedros Convexos E Regulares
Elas representam sólidos, e são exemplos de poliedros De um modo geral, chamamos de Poliedro à região do espaço limitada por polígonos planos, e tais que cada uma das arestas desses...
- Diedros Questões Vestibular
Diedros Dois semiplanos não-coplanares, com origem numa mesma reta, determinam uma figura geométrica chamada ângulo diédrico, ou simplesmente diedro: Secção reta de um diedro Chamamos de seção...
