Vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos.
Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice comum, que é o vértice da pirâmide.
classificação das pirâmides
Pirâmide regular
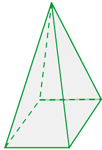
A pirâmide regular tem na base um polígono regular e sus faces laterais iguais.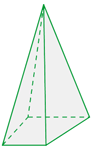
A pirâmide irregular tem como base um polígono irregular.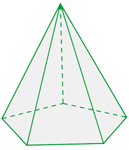
A pirâmide convexa tem como base um polígono convexo.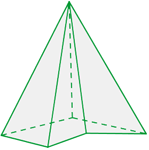
A pirâmide convexa tem como base um polígono côncavo.
Na pirâmide reta o vértice tem a sua projeção coincidente com o centro da base.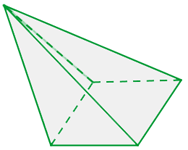
Na pirâmide oblíqua a projeção do vértice não coincide com o cento do polígono da base.Classificação das pirâmides segundo sua base
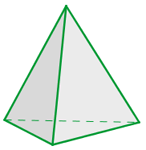
Sua base é um triângulo.
Sua base é um quadrado.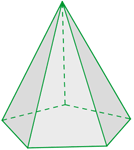
Sua base é um pentágono.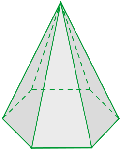
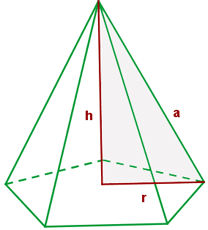
Calculamos a aresta lateral da pirâmide, conhecendo a altura e o raio da base o raio da circunferência circunscrita, aplicando el teorema de Pitágoras no triângulo sombreado:
Área da base
Volume
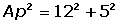
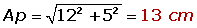
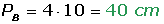
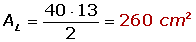
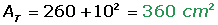
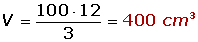2) Calcula a área lateral, total e o volume de una pirâmide hexagonal de 16 cm de aresta básica e 28 cm de aresta lateral.
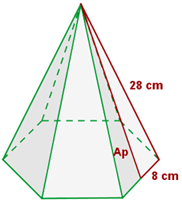
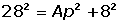
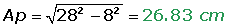
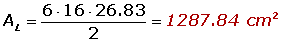
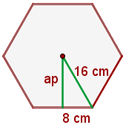
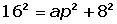
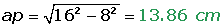
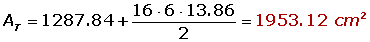
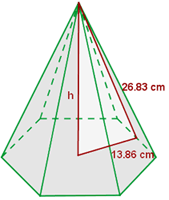
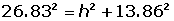
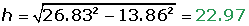
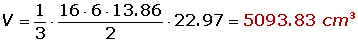
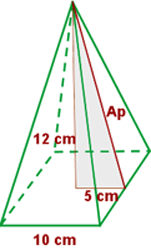
O apótema é o valor da hipotenusa do triangulo que parte da altura e segue para o meio da aresta. Para calcula-lo, basta usar o teorema de Pitágoras, onde o um dos catetos é a altura e o outro é a metade da aresta:
a) 36cm² b) 48cm² c) 54cm² d) 72cm² e) 108cm²
Para resolver é só ler bem a questão e saber interpretar, é bem simples de resolvé-la basta multiplicar a área (que o problema nos dá ) pelos lados do hexágono ( 6 ),ou seja , 12 X 6 = 72cm²
- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- Cilindro Questões De Vestibular
Cilindro Consideremos um círculo de centro O e raio r num plano , e um segmento de reta , cuja reta suporte intercepta em Q. Temos segmentos de reta paralelos e congruentes a , cada um deles com uma das extremidades num ponto do círculo e a outra...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- Diedros Questões Vestibular
Diedros Dois semiplanos não-coplanares, com origem numa mesma reta, determinam uma figura geométrica chamada ângulo diédrico, ou simplesmente diedro: Secção reta de um diedro Chamamos de seção...
Vestibular
pirâmides questões vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos.
Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice comum, que é o vértice da pirâmide.
classificação das pirâmides
Pirâmide regular
A pirâmide regular tem na base um polígono regular e sus faces laterais iguais.
Pirâmide irregular
A pirâmide irregular tem como base um polígono irregular.
Pirâmide convexa
A pirâmide convexa tem como base um polígono convexo.
Pirâmide côncava
A pirâmide convexa tem como base um polígono côncavo.
Pirâmide reta
Na pirâmide reta o vértice tem a sua projeção coincidente com o centro da base.
Pirâmide obliqua
Na pirâmide oblíqua a projeção do vértice não coincide com o cento do polígono da base.
Pirâmide triangular
Sua base é um triângulo.
Pirâmide quadrangular
Sua base é um quadrado.
Pirâmide pentagonal
Sua base é um pentágono.
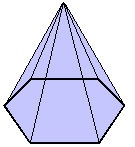
Pirâmide hexagonal
Sua base é um hexágono.
Cálculo da aresta lateral de uma pirâmide
Calculamos a aresta lateral da pirâmide, conhecendo a altura e o raio da base o raio da circunferência circunscrita, aplicando el teorema de Pitágoras no triângulo sombreado:
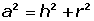
Cálculo da apótema lateral de uma pirâmide
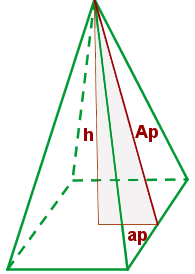
Calculamos a apótema lateral da pirâmide conhecendo a altura e a apótema da base, aplicando o teorema de Pitágoras no triângulo sombreado:
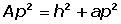
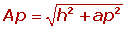
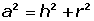
Cálculo da apótema lateral de uma pirâmide
Calculamos a apótema lateral da pirâmide conhecendo a altura e a apótema da base, aplicando o teorema de Pitágoras no triângulo sombreado:
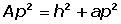
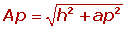
Área da base
A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:
onde P: perímetro do polígono e a: apótema do polígono.
Área lateral
É a soma de todas as áreas laterais, ou seja:
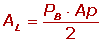onde: PB é o perímetro de base e Ap é o apótema lateral da pirâmide.
Área total
Soma da área lateral com a área da base.
At = Al + Ab
Volume
O volume de uma pirâmide é dado pela expressão:
onde Ab: área da base (depende do polígono) e h: altura da pirâmide.
Questões propostas pirâmides
1) Calcule a área lateral, total e o volume de una pirâmide quadrangular de 10 cm de aresta e 12 cm de altura.
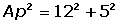
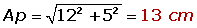
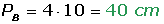
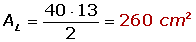
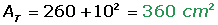
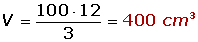
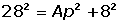
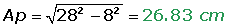
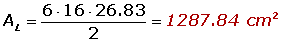
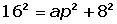
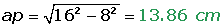
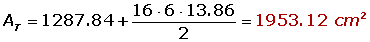
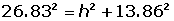
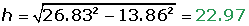
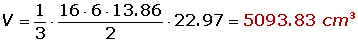
3) Numa pirâmide quadrangular, a aresta mede 18cm e a altura é equivalente a 12 cm. Calcule o volume, a apótema.
Volume
Basta multiplicar a área da base (aresta x aresta) e dividir por 3. Veja:
O apótema é o valor da hipotenusa do triangulo que parte da altura e segue para o meio da aresta. Para calcula-lo, basta usar o teorema de Pitágoras, onde o um dos catetos é a altura e o outro é a metade da aresta:4) ( UNIV ) As faces laterais de uma pirâmide hexagonal regular são triângulos isósceles com área de 12cm² cada.A área lateral do sólido vale:
a) 36cm² b) 48cm² c) 54cm² d) 72cm² e) 108cm²
Para resolver é só ler bem a questão e saber interpretar, é bem simples de resolvé-la basta multiplicar a área (que o problema nos dá ) pelos lados do hexágono ( 6 ),ou seja , 12 X 6 = 72cm² Resposta : letra D
4) Calcular a área lateral de uma pirâmide quadrangular regular que tem 12cm de altura e 40cm de perímetro da base.
5) Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 24cm e que o apótema da pirâmide mede 26cm?
6) A área lateral de uma pirâmide quadrangular regular de altura 4m e de área da base 64m² vale:
7) Uma pirâmide quadrada tem todas as arestas medindo 2. A altura mede:
8) (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
9) (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
10) (Unirio) As arestas laterais de uma pirâmide reta medem 15cm, e a sua base é um quadrado cujos lados medem 18cm. A altura dessa pirâmide, em cm, é igual a:
a) 2?7 b) 3? 7 c) 4?7 d) 5?7
11) (FEI - MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h - x sejam iguais.
12) (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano ABC sabendo-se que VA = VB = VC = 1m.
13) (UFRS) A base de uma pirâmide tem área igual a 225cm². A 2/3 do vértice, corta-se a pirâmide por um plano paralelo à base. A área da secção é igual a:
a) 30 b) 50 c) 70 d) 90 e) 100
Gabarito:
4) 260cm² 5) 1440cm² 6) 64?2 m² 7) ?2 8) D 9) C 10) B 11) h?2 /2 12)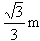
13) E
5) Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 24cm e que o apótema da pirâmide mede 26cm?
6) A área lateral de uma pirâmide quadrangular regular de altura 4m e de área da base 64m² vale:
7) Uma pirâmide quadrada tem todas as arestas medindo 2. A altura mede:
8) (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
9) (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
10) (Unirio) As arestas laterais de uma pirâmide reta medem 15cm, e a sua base é um quadrado cujos lados medem 18cm. A altura dessa pirâmide, em cm, é igual a:
a) 2?7 b) 3? 7 c) 4?7 d) 5?7
11) (FEI - MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h - x sejam iguais.
12) (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano ABC sabendo-se que VA = VB = VC = 1m.
13) (UFRS) A base de uma pirâmide tem área igual a 225cm². A 2/3 do vértice, corta-se a pirâmide por um plano paralelo à base. A área da secção é igual a:
a) 30 b) 50 c) 70 d) 90 e) 100
Gabarito:
4) 260cm² 5) 1440cm² 6) 64?2 m² 7) ?2 8) D 9) C 10) B 11) h?2 /2 12)
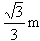13) E- Cones Questões Vestibular
Artigo sobre áreas e volume de um cone, classificação dos cones com questões resolvidas para um melhor um melhor melhor aprendizado. Cones Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. O cone será formado por...
- Cilindro Questões De Vestibular
Cilindro Consideremos um círculo de centro O e raio r num plano , e um segmento de reta , cuja reta suporte intercepta em Q. Temos segmentos de reta paralelos e congruentes a , cada um deles com uma das extremidades num ponto do círculo e a outra...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- Diedros Questões Vestibular
Diedros Dois semiplanos não-coplanares, com origem numa mesma reta, determinam uma figura geométrica chamada ângulo diédrico, ou simplesmente diedro: Secção reta de um diedro Chamamos de seção...