Vestibular
Elas representam sólidos, e são exemplos de poliedros
De um modo geral, chamamos de Poliedro à região do espaço limitada por polígonos planos, e tais que cada uma das arestas desses polígonos pertença a dois e somente dois deles.
As relações de Euler são duas importantes relações entre o número F de faces, o número V de vértices, o número A de arestas e o número m de ângulos entre as arestas.
F + V = A + 2, m = 2 A
Na tabela abaixo, você pode observar o cumprimento de tais relações para os cinco (5) poliedros regulares convexos.
Aplicação da relação de Euler
Exemplo:
Um poliedro convexo tem 6 faces triangulares e 3 faces quadrangulares. Determinar o número de arestas, o número de vértices e a soma dos ângulos de todas as faces.
Solução:
Aparentemente, o número de arestas deveria ser (6 x 3 + 3 x 4) = 30, mas como cada aresta é contada duas vezes, então o número de arestas é 30/2 = 15.
Logo A = 15.
O número de faces é F = 6 + 3 = 9
como V - A + F = 2
V = A + 2 - F
V = 15 + 2 - 9
V = 8.
- QuestÕes De Concursos, Vestibulares E NotÍcias De Concursos Em Aberto: Poliedros Questões Vestibular
...
- Tetraedros Regulares Questões
Artigo sobre tetraedros, área e volume dos tetraedros com questões resolvidas e propostas. O tetraedro regular é um sólido platônico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros (triângulos...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
- Polígonos - Geometria
Um polígono é uma figura geométrica plana limitada por uma linha poligonal fechada. A palavra "polígono" advém do grego e quer dizer muitos (poli) e ângulos (gono). Elementos de um polígonoUm polígono possui os seguintes elementos:?...
Vestibular
Poliedros convexos e regulares


Elas representam sólidos, e são exemplos de poliedros
De um modo geral, chamamos de Poliedro à região do espaço limitada por polígonos planos, e tais que cada uma das arestas desses polígonos pertença a dois e somente dois deles.
Veja:
- Polígono = figura plana
- Poliedro = sólido, em 3 dimensões, no espaço, formado por polígonos
- Arestas = lados dos polígonos que formam o poliedro
- Vértices = os pontos onde as arestas se interceptam
- Faces = cada um dos polígonos que formam o poliedro

Mas atenção: não são poliedros os sólidos que possuem formas arredondadas, como o cilindro e o cone:
Os poliedros são convexos quando se encontram todos para o mesmo lado em relação ao plano de qualquer uma das suas faces, ou seja, quando as suas faces deixam sempre as demais no mesmo semiespaço. Complicado? Vamos entender melhor isso!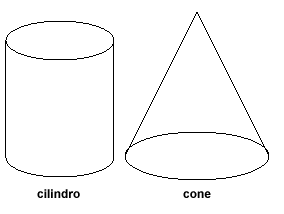
Poliedros convexos
Considere um poliedro e uma de suas faces: um octaedro, por exemplo. Imagine um plano apoiado nessa face. O poliedro ficou todo de um lado só desse plano? Então ele é convexo! Veja: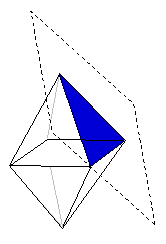
Poliedro convexo 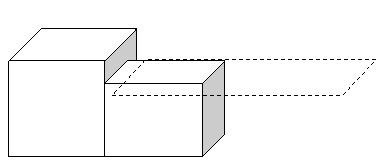
Poliedro não convexo Características dos poliedros convexos
Notações para poliedros convexos: V: Número de vértices, F: Número de faces, A: Número de arestas, n: Número de lados da região poligonal regular (de cada face), a: Medida da aresta A e m: Número de ângulos entre as arestas do poliedro convexo.Característica do
poliedro convexoMedida da característica Relação de Euler V + F = A + 2 Número m de ângulos diedrais m = 2 A Ângulo diedral 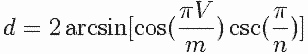
Raio do círculo inscrito 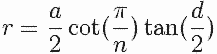
Raio do círculo circunscrito 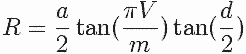
Área da superfície externa 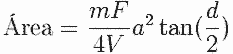
Volume do sólido poliédrico 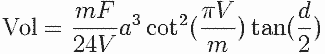 ClassificaçãoOs poliedros convexos possuem nomes especiais de acordo com o número de faces, como por exemplo:
ClassificaçãoOs poliedros convexos possuem nomes especiais de acordo com o número de faces, como por exemplo:- tetraedro: quatro faces
- pentaedro: cinco faces
- hexaedro: seis faces
- heptaedro: sete faces
- octaedro: oito faces
- icosaedro: vinte face
Polígonos regularesVamos lembrar o conceito de polígono regular: aquele em que todos os lados são congruentes (iguais) e todos os ângulos são também congruentes.
Então, um poliedro é regular se suas faces são polígonos regulares, todos com o mesmo número de lados e, em cada vértice do poliedro, encontram-se (convergem) sempre o mesmo número de arestas.
Existem apenas cinco poliedros regulares:
As relações de Euler são duas importantes relações entre o número F de faces, o número V de vértices, o número A de arestas e o número m de ângulos entre as arestas.
F + V = A + 2, m = 2 A
Na tabela abaixo, você pode observar o cumprimento de tais relações para os cinco (5) poliedros regulares convexos.
.
| Poliedro regular convexo | Cada face é um | Faces (F) | Vértices (V) | Arestas (A) | Ângulos entre as arestas (m) |
|---|---|---|---|---|---|
| Tetraedro | triângulo equilátero | 4 | 4 | 6 | 12 |
| Hexaedro | quadrado | 6 | 8 | 12 | 24 |
| Octaedro | triângulo equilátero | 8 | 6 | 12 | 24 |
| Dodecaedro | pentágono regular | 12 | 20 | 30 | 60 |
| Isocaedro | triângulo equilátero | 20 | 12 | 30 | 60 |
Aplicação da relação de Euler
Exemplo:
Um poliedro convexo tem 6 faces triangulares e 3 faces quadrangulares. Determinar o número de arestas, o número de vértices e a soma dos ângulos de todas as faces.
Solução:
Aparentemente, o número de arestas deveria ser (6 x 3 + 3 x 4) = 30, mas como cada aresta é contada duas vezes, então o número de arestas é 30/2 = 15.
Logo A = 15.
O número de faces é F = 6 + 3 = 9
como V - A + F = 2
V = A + 2 - F
V = 15 + 2 - 9
V = 8.
Poliedros platônicos
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Assim, nas figuras acima, o primeiro poliedro é platônico e o segundo, não-platônico.
- QuestÕes De Concursos, Vestibulares E NotÍcias De Concursos Em Aberto: Poliedros Questões Vestibular
...
- Tetraedros Regulares Questões
Artigo sobre tetraedros, área e volume dos tetraedros com questões resolvidas e propostas. O tetraedro regular é um sólido platônico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros (triângulos...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
- Polígonos - Geometria
Um polígono é uma figura geométrica plana limitada por uma linha poligonal fechada. A palavra "polígono" advém do grego e quer dizer muitos (poli) e ângulos (gono). Elementos de um polígonoUm polígono possui os seguintes elementos:?...
