Vestibular
Nesse artigo estudaremos o binômio de Newton, desenvolvimento do binômio de Newton e coeficientes binominais com exercícios resolvidos e propostos de vestibulares e concursos anteriores.
1. Introdução Binômio de Newton
O binômio de Newton desenvolvido pelo célebre Isaac Newton serve para o cálculo de um número binomial do tipo (a + b)n .
Se n for 2, fica simples é apenas decorar que (a+b)² = a² + 2ab + b², ou seja, o quadrado do primeiro mais duas vezes o primeiro pelo segundo mais o quadrado do segundo. Porém quando o valor de n é grande, este processo gradativo de cálculo é muito trabalhoso. O binômio de Newton veio pra facilitar esses cálculos, pois com ele calculamos a enésima potência de um binômio. Para esse método, porém, é necessário saber o que são coeficientes binomiais, algumas de suas propriedades e o triângulo de Pascal.
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3 a2b + 3ab2 + b3(a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
(a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
(a + b)5 = a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5ab4 + b5
Exemplo 1:
Determine o polinômio correspondente ao desenvolvimento da expressão (3x +2)4 .
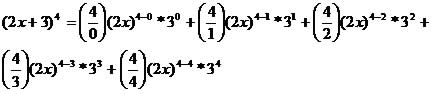 (2x + 3)4 = (2x)4 * 1 + (2x)³ * 3 + (2x)² * 9 + (2x)¹*27 + (2x)0 * 81
(2x + 3)4 = (2x)4 * 1 + (2x)³ * 3 + (2x)² * 9 + (2x)¹*27 + (2x)0 * 81
(2x + 3)4 = 16x4 + 24x³ + 36x² + 54x + 81
Também podemos resolver pelo método da distribuição. Observe:
(2x + 3)4 = (2x + 3) * (2x + 3) * (2x + 3) * (2x + 3) = 16x4 + 24x³ + 36x² + 54x + 81
Porém, para situações nas quais o expoente indicado apresenta valores mais elevados, é aconselhado utilizar o binômio de Newton no desenvolvimento da expressão.
Para desenvolvermos uma expressão do tipo (2x ? 3)4 , devemos alternar os sinais, iniciando com o sinal de positivo. A expressão (2x ? 3)4 ficaria da seguinte forma:
(2x + 3)4 = 16x4 - 24x³ + 36x² - 54x + 81 
Pela fórmula do termo geral, podemos escrever:
05. (CESGRANRIO) O coeficiente de x4 no polinômio P(x) = (x + 2)6 é:
a) 64 b) 60 c) 12 d) 4 e) 24
a) 1 b) -1 c) 0 d) 104 e) 2
a) 10 b) -10 c) 20 d) -20 e) 36
10. O desenvolvimento de (y-2)7 possui:
a) 7 termos
b) 560 por coeficiente de y3
c) coeficiente negativo se o expoente de y for ímpar
d) coeficiente de y6 igual ao coeficiente de y
e) 6 termos
11. (F.Ibero Americana-SP) Se a³ + 6a²b + 12ab² + 8b³ - 12a²b + 6ab² - b³ = - 1, calcule o valor de a + b.
a) -3 b) -2 c) -1 d) 0 e) 1
12. (U. Estácio de Sá - RJ) O valor de n na soma dos coeficientes do desenvolvimento (a + b)n = 2048 é:
a) 10 b) 11 c) 12 d) 13 e) 14
Gabarito:

- Binômio De Newton
Denomina-se Binômio de Newton , a todo binômio da forma (a + b)n , sendo n um número natural . Exemplo: B = (3x - 2y)4 ( onde a = 3x, b = -2y e n = 4 [grau do binômio] ).Nota 1: Isaac Newton - físico e matemático inglês(1642 - 1727). Suas...
- Polinômios Questões Vestibular
Adição e subtração de polinômios O procedimento utilizado na adição e subtração de polinômios envolve técnicas de redução de termos semelhantes, operações envolvendo sinais iguais e sinais diferentes e jogo de sinal. Observe os exemplos:...
- Questões Resolvidas De Progressão Aritmética
Lista de questões resolvidas sobre progressão aritmética de vestibulares anteriores. Exercícios resolvidos de P.A 1) Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, para que a soma...
- Progressão Aritmética(p.a)
Nesse artigo será abordado Progressão aritmética com vários exemplos para um melhor aprendizado. 1 - Conceito de Progressão Aritmética - PA Chama-se Progressão Aritmética ? P.A ? à toda sequência numérica cujos termos a partir do segundo,...
- Triângulo De Pascal E Suas Propriedades
Nesse artigo, estudaremos o triângulo de Pascal e suas propriedades com exercícios resolvidos O triângulo de Pascal recebeu esse nome devido ao matemático Blaise Pascal (1623-1662). O triângulo é infinito e simétrico, e seus lados esquerdo...
Vestibular
questões resolvidas Análise combinatória
Nesse artigo estudaremos o binômio de Newton, desenvolvimento do binômio de Newton e coeficientes binominais com exercícios resolvidos e propostos de vestibulares e concursos anteriores.
1. Introdução Binômio de Newton
O binômio de Newton desenvolvido pelo célebre Isaac Newton serve para o cálculo de um número binomial do tipo (a + b)n .
Se n for 2, fica simples é apenas decorar que (a+b)² = a² + 2ab + b², ou seja, o quadrado do primeiro mais duas vezes o primeiro pelo segundo mais o quadrado do segundo. Porém quando o valor de n é grande, este processo gradativo de cálculo é muito trabalhoso. O binômio de Newton veio pra facilitar esses cálculos, pois com ele calculamos a enésima potência de um binômio. Para esse método, porém, é necessário saber o que são coeficientes binomiais, algumas de suas propriedades e o triângulo de Pascal.
Nota:
exemplos de desenvolvimento de Binômio de Newton:
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3 a2b + 3ab2 + b3(a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
(a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
(a + b)5 = a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5ab4 + b5
2. Fórmula do termo geral do desenvolvimento de (a + b)n
Observando os termos do desenvolvimento de (a + b)n, notamos que cada um deles é da forma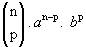 .
.
Observando os termos do desenvolvimento de (a + b)n, notamos que cada um deles é da forma
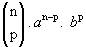 .
.- Quando p = 0 temos o 1º termo:
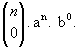
- Quando p = 1 temos o 2º termo:

- Quando p = 2 temos o 3º termo:

- Quando p = 3 temos o 4º termo:

- Quando p = 4 temos o 5º termo:
 Percebemos, então, que um termo qualquer T de ordem p + 1pode ser expresso por:
Percebemos, então, que um termo qualquer T de ordem p + 1pode ser expresso por: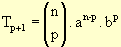
Termo Central ou Médio: é aquele que fica no meio, se o desenvolvimento for de grau par. ( p = n/2 )
Termo Independente da variável é aquele cujo expoente desta variável é igual a zero.(b0)
Exemplo 1:
Determine o polinômio correspondente ao desenvolvimento da expressão (3x +2)4 .
Temos:
(3x +2)4 = (40)(3x)4.20 + (41)(3x)3.21 + (42)(3x)2.22 + (43)(3x)1.23 + (44)(3x)0.24.
Isto é:
(3x +2)4 = 81x4 + 216x3 + 216x2 +96x + 16
Exemplo 2:
Determine o polinômio correspondente ao desenvolvimento da expressão
(2x + 3)4.
(2x + 3)4.
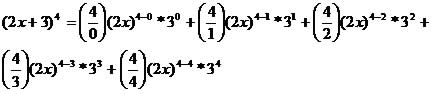
(2x + 3)4 = 16x4 + 24x³ + 36x² + 54x + 81
Também podemos resolver pelo método da distribuição. Observe:
(2x + 3)4 = (2x + 3) * (2x + 3) * (2x + 3) * (2x + 3) = 16x4 + 24x³ + 36x² + 54x + 81
Porém, para situações nas quais o expoente indicado apresenta valores mais elevados, é aconselhado utilizar o binômio de Newton no desenvolvimento da expressão.
Para desenvolvermos uma expressão do tipo (2x ? 3)4 , devemos alternar os sinais, iniciando com o sinal de positivo. A expressão (2x ? 3)4 ficaria da seguinte forma:
(2x + 3)4 = 16x4 - 24x³ + 36x² - 54x + 81
3. Coeficientes binomiais
Dados dois números naturais n e p, chama-se coeficientes binomiais n sobre p, indicado por 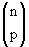 , ao número definido por:
, ao número definido por:
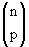 , ao número definido por:
, ao número definido por:
O coeficiente binomial também é chamado de número binomial. Por analogia com as frações, dizemos que n é o seu numerador e p, o denominador. Podemos escrever:
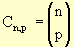 |
Assim, por exemplo, temos:
(107) = C10,7 = 10! / [7! 3!] = 120
(73)= C7,3 = 7! / [3!4!] = 35
Casos particulares:
(n0)= n! / [0!n!] = n! / [1 n!] = 1
(n1)= n! / [1!(n-1)!] = n(n-1)! / (n-1)! = n
(nn)= n! / [n! 0!] = 1
Então, por exemplo, temos que:
(30)= 1
(51)= 5
(66)= 1
(107) = C10,7 = 10! / [7! 3!] = 120
(73)= C7,3 = 7! / [3!4!] = 35
Casos particulares:
(n0)= n! / [0!n!] = n! / [1 n!] = 1
(n1)= n! / [1!(n-1)!] = n(n-1)! / (n-1)! = n
(nn)= n! / [n! 0!] = 1
Então, por exemplo, temos que:
(30)= 1
(51)= 5
(66)= 1
Propriedades dos coeficientes binomiais
1ª) |
|
Coeficientes binomiais como esses, que tem o mesmo numerador e a soma dos denominadores igual ao numerador, são chamados complementares.
Exemplos:
 | 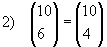 |  |
2ª) |
|
Essa igualdade é conhecida como relação de Stifel (Michael Stifel, matemático alemão, 1487 - 1567).
Exemplos:
 | 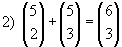 |  |
Extraido de :
http://www.somatematica.com.br/emedio/binomio/binomio2.php
Olá,
Saiba quais são as principais causas da queda de cabelo e veja como evitar
esse mal que afeta homens e mulheres, sem gastar com produtos caros.
Acesse Agora: http://www.pareaquedadecabelo.com/af/5190
Exercícios resolvidos e propostos com gabarito Binômio de Newton
01. Desenvolvendo o binômio (2x - 3y)3n , obtemos um polinômio de 16 termos .
Qual o valor de n?
Solução:
Ora, se o desenvolvimento do binômio possui 16 termos, então o expoente do binômio é igual a 15.
Logo, 3n = 15 de onde conclui-se que n = 5.
Ora, se o desenvolvimento do binômio possui 16 termos, então o expoente do binômio é igual a 15.
Logo, 3n = 15 de onde conclui-se que n = 5.
02. Determine o termo independente de x no desenvolvimento de (x + 1/x )6 .
Solução:
Sabemos que o termo independente de x é aquele que não depende de x, ou seja, aquele que não possui x.
Temos no problema dado: a = x , b = 1/x e n = 6.Pela fórmula do termo geral, podemos escrever:
Tp+1 = C6,p . x6-p . (1/x)p = C6,p . x6-p . x-p = C6,p . x6-2p .
Ora, para que o termo seja independente de x, o expoente desta variável deve ser zero, pois x0 = 1. Logo, fazendo 6 - 2p = 0, obtemos p=3. Substituindo então p por 6, teremos o termo procurado. Temos então:
T3+1 = T4 = C6,3 . x0 = C6,3 = 6! /[(6-3)! . 3! ] = 6.5.4.3! / 3!.3.2.1 = 20.Logo, o termo independente de x é o T4 (quarto termo) que é igual a 20.
Ora, para que o termo seja independente de x, o expoente desta variável deve ser zero, pois x0 = 1. Logo, fazendo 6 - 2p = 0, obtemos p=3. Substituindo então p por 6, teremos o termo procurado. Temos então:
T3+1 = T4 = C6,3 . x0 = C6,3 = 6! /[(6-3)! . 3! ] = 6.5.4.3! / 3!.3.2.1 = 20.Logo, o termo independente de x é o T4 (quarto termo) que é igual a 20.
03. (UF. VIÇOSA) A soma dos coeficientes do desenvolvimento de (2x + 3y)m é 625. O valor de m é:
a) 5 b) 6 c)10 d) 3 e) 4
04. Calcule a soma dos coeficientes do desenvolvimento de (x - 3y)7 .
a) -128 b) - 256 c) 56 d) 128 e) 256
a) 64 b) 60 c) 12 d) 4 e) 24
06. A soma dos coeficientes numéricos dos termos do desenvolvimento de (x - y)104 é:
a) 1 b) -1 c) 0 d) 104 e) 2
07. Calcule o 4° termo no desenvolvimento de (2x ? 1)6
08. (FGV-SP) Desenvolvendo-se a expressão [(x + 1/x) . (x - 1/x)]6 , obtém-se como termo independente de x o valor:
a) 10 b) -10 c) 20 d) -20 e) 36
09. Os 3 primeiros coeficientes no desenvolvimento de (x2 + 1/(2x))n estão em progressão aritmética.O valor de n é:
a) 8 b) 6 c) 4 d) 7 e) 12
a) 8 b) 6 c) 4 d) 7 e) 12
10. O desenvolvimento de (y-2)7 possui:
a) 7 termos
b) 560 por coeficiente de y3
c) coeficiente negativo se o expoente de y for ímpar
d) coeficiente de y6 igual ao coeficiente de y
e) 6 termos
11. (F.Ibero Americana-SP) Se a³ + 6a²b + 12ab² + 8b³ - 12a²b + 6ab² - b³ = - 1, calcule o valor de a + b.
a) -3 b) -2 c) -1 d) 0 e) 1
12. (U. Estácio de Sá - RJ) O valor de n na soma dos coeficientes do desenvolvimento (a + b)n = 2048 é:
a) 10 b) 11 c) 12 d) 13 e) 14
Gabarito:
1) n = 5 2) 20 3) E 4) A 5) B 6) C 7) 20 8) D 9) A 10) B 11) E 12) B
veja também:
Questões Permutação com repetição
Triângulo de Pascal e suas propriedades
questões resolvidas fatorial
Questões permutação simples
Questões Fuvest matemática de vestibulares anteriores
Questões Permutação com repetição
http://aprendaadesenhardozero.com.br/cursoonline/?

Curso Online de Desenho ? Aprenda a Desenhar do Zero
Ivan, estou feliz com o curso, sempre quis desenhar, mas o tempo e muito curto, e retomei esse sonho com o curso, aos poucos estou conseguindo cumprir todas as tarefas e vejo muitas melhorias nos meus trabalhos, Ivan suas explicações são...
APRENDAADESENHARDOZERO.COM.BR
- Binômio De Newton
Denomina-se Binômio de Newton , a todo binômio da forma (a + b)n , sendo n um número natural . Exemplo: B = (3x - 2y)4 ( onde a = 3x, b = -2y e n = 4 [grau do binômio] ).Nota 1: Isaac Newton - físico e matemático inglês(1642 - 1727). Suas...
- Polinômios Questões Vestibular
Adição e subtração de polinômios O procedimento utilizado na adição e subtração de polinômios envolve técnicas de redução de termos semelhantes, operações envolvendo sinais iguais e sinais diferentes e jogo de sinal. Observe os exemplos:...
- Questões Resolvidas De Progressão Aritmética
Lista de questões resolvidas sobre progressão aritmética de vestibulares anteriores. Exercícios resolvidos de P.A 1) Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro termo, para que a soma...
- Progressão Aritmética(p.a)
Nesse artigo será abordado Progressão aritmética com vários exemplos para um melhor aprendizado. 1 - Conceito de Progressão Aritmética - PA Chama-se Progressão Aritmética ? P.A ? à toda sequência numérica cujos termos a partir do segundo,...
- Triângulo De Pascal E Suas Propriedades
Nesse artigo, estudaremos o triângulo de Pascal e suas propriedades com exercícios resolvidos O triângulo de Pascal recebeu esse nome devido ao matemático Blaise Pascal (1623-1662). O triângulo é infinito e simétrico, e seus lados esquerdo...

 e p + k = n então
e p + k = n então 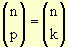
 p-1
p-1 