Vestibular
Artigo com questões sobre relações métricas no triângulo retângulo resolvidas e propostas
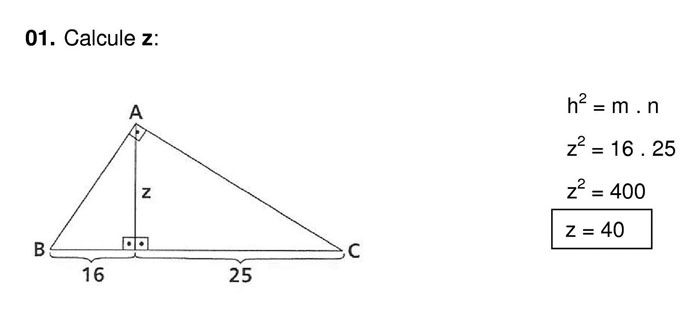


03. No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:






- Geometria Plana - Matéria Completa
Artigos de "Geometria Plana" - área do triângulo retângulo questões - perímetro de figuras planas questões- Perímetro das figuras geométricas - área do quadrado questões vestibular - semelhança de figuras planas - área...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- Relações Trigonométricas Num Triângulo Retângulo Questões Vestibular
1) Encontre a medida RA sabendo que tg  = 3.3 = 9 / x3x = 9x = 3(RA)² = 9² + 3²(RA)² = 90(RA) = 2) No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14)...
- Relações Trigonométricas No Triângulo Retângulo Exemplos
Estudaremos agora as relações trigonométricas no triângulo retângulo com exemplos para um melhor aprendizado. Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria...
- Aplicações Do Teorema De Pitágoras No Cotidiano
O Teorema de Pitágoras está presente em diversas situações no cotidiano. Vamos através de exercícios demonstrar algumas aplicações. 1) Dois navios, A e B, partem de um ponto O e seguem em direção perpendicular um ao outro. O navio...
Vestibular
questões de relações métricas no triângulo retângulo
Artigo com questões sobre relações métricas no triângulo retângulo resolvidas e propostas


DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...
Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de
DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR
03. No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:

Resolução:
Pelo teorema de Pitágoras temos:
x2 = 52 + 122
x2 = 169
x = 13
Aplicando as relações de projeções de catetos, vem:
52 = x . z
13 . z = 25
z = 25 / 13
122 = x . t
13 . t = 144
t = 144 / 13
04. Dado o triângulo retângulo ABC, reto em A, representado na figura abaixo, calcule os valores desconhecidos (x, m, n e h).

x = 4 m,
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
h = 12/5 m = 2,4 m,
m = 9/5 m = 1,8 m,
n = 16/5 m =3,2 m
05. Em um triangulo retângulo, sua altura(h) é = 5 e sua hipotenusa(a) é =26. Calcule o cateto b (cateto maior).
Vamos recordar as relações métricas em um triângulo retângulo:
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5?26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= ?26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = ? 5² . 26
b = 5 ? 26
logo, o cateto maior b = 5 ?26 m
a = m + n
b² = a.m
c² = a.n
b.c = a.h
h² = m.n
a² = b² + c²
no exercício dado, sabemos que
h = 5
a = 26
observe que nenhuma das relações métricas envolve apenas essas duas medidas
vamos ter que encontrar um caminho.
Façamos, primeiro:
m + n = a
m + n = 26
n = 26 - m (I)
b² = a . m (onde m é a maior das projeções)
b² = 26m (II)
c² = a.n
c² = 26n --> c² = 26(26 - m) --> c² = 676 - 26m (III)
b . c = a . h
b . c = 26 . 5
b . c = 130
eleva ao quadrado:
b² c² = 16900
substitui (II) e (III)
26m ( 676 - 26m) = 16900
17576m - 676m² = 16900
676m² - 17576m + 16900 = 0 --> simplifica por 676
m² - 26m + 25 = 0
resolve por báskara ou pela soma e produto:
m' = 25
m" = 1 (despreza por ser o menor)
b² = 26m (II)
b² = 25 . 26 ==> b = 5?26 m que é o cateto maior
como a = m + n
n = 1
c² = 26n --> c² = 26 --> c= ?26 m que é o cateto menor
Poderíamos também usar outras duas relações métricas:
h = m.n ---> m . n = 25 (I)
a = m + n --> m + n = 26 donde m = 26 - n (II)
Substitui (II) em (I)
( 26 - n ) . n = 25
n² - 26n + 25 = 0
resolvendo por báskara ou pela soma e produto:
n' = 1
n" = 25 (despreza, pois consideramos inicialmente que m é a maior)
como
m = 26 - n (II)
m = 26 - 1
m = 25
assim, sabendo que
b² = a.m
temos
b² = 26 . 25
b = ? 5² . 26
b = 5 ? 26
logo, o cateto maior b = 5 ?26 m


08. No triângulo retângulo abaixo determinar a hipotenusa, as projeções dos catetos sobre a hipotenusa e a altura relativa a hipotenusa:

Resolução:
Pelo teorema de Pitágoras temos:
x2 = 52 + 122
x2 = 169
x = 13
Aplicando as relações de projeções de catetos, vem:
52 = x . z
13 . z = 25
z = 25 / 13
122 = x . t
13 . t = 144
t = 144 / 13
Aplicando a relação do produto dos catetos, vem:
x . y = 5 . 12
13 . y = 60
y = 60 / 13
Agora pratique:
09. (FATEC-SP) Se os catetos de um triângulo retângulo T, medem, respectivamente, 12 cm e 5 cm, então a altura de T relativa à hipotenusa é:
a) 12/5 m b) 5/13 m c) 12/13 m d) 25/13 m e) 60/13 m
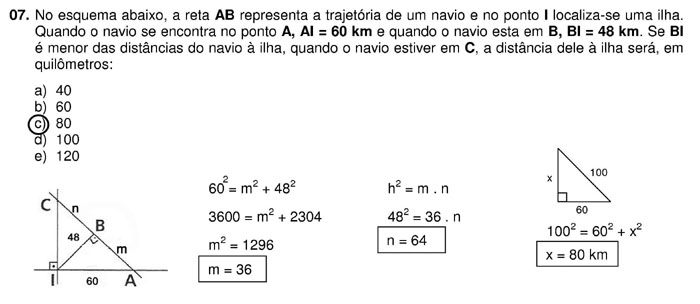
10. Sabe-se que a altura de um triângulo retângulo mede 48 cm e a medida de um dos catetos é igual a 60 cm. A projeção desse cateto sobre a hipotenusa é:
a) 33 b) 34 c) 35 d) 36 e) 37
a) 33 b) 34 c) 35 d) 36 e) 37
11. (Cesgranrio-RJ) Num triângulo retângulo em A, a altura relativa à hipotenusa mede 12, e o menor dos segmentos que ela determina sobre a hipotenusa, 9. O menor lado do triângulo mede:

a) 12,5 b) 13 c) 15 d) 16 e) 16,5
DATAHOSTING.COM.BR|DE http://www.datahosting.com.br/afiliados/ok.php?id=8893

HOSPEDAGEM DE SITES R$14,90 com 10GB de Espaço e 150GB de Tráfego, Construtor de Sites e...
Hospedagem de sites com planos gigantes a partir de R$14,90, 10GB de espaço, 150Gb de tráfego de
DATAHOSTING.COM.BR|DE WWW.DATAHOSTING.COM.BR
- Geometria Plana - Matéria Completa
Artigos de "Geometria Plana" - área do triângulo retângulo questões - perímetro de figuras planas questões- Perímetro das figuras geométricas - área do quadrado questões vestibular - semelhança de figuras planas - área...
- área Do Triângulo Retângulo Questões
Estudaremos nesse artigo sobre a área do triângulo retângulo com questões resolvidas para um melhor aprendizado. área do triângulo retângulo A área do triângulo retângulo é dada por onde h é a altura do triângulo, b a...
- Relações Trigonométricas Num Triângulo Retângulo Questões Vestibular
1) Encontre a medida RA sabendo que tg  = 3.3 = 9 / x3x = 9x = 3(RA)² = 9² + 3²(RA)² = 90(RA) = 2) No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14)...
- Relações Trigonométricas No Triângulo Retângulo Exemplos
Estudaremos agora as relações trigonométricas no triângulo retângulo com exemplos para um melhor aprendizado. Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria...
- Aplicações Do Teorema De Pitágoras No Cotidiano
O Teorema de Pitágoras está presente em diversas situações no cotidiano. Vamos através de exercícios demonstrar algumas aplicações. 1) Dois navios, A e B, partem de um ponto O e seguem em direção perpendicular um ao outro. O navio...
