Vestibular
Artigo com questões de vestibular sobre poliedros resolvidas e propostas
Resolução:
7) Um poliedro convexo tem 16 faces. De um de seus vértices partem 5 arestas , dos outros 5
vértices partem 4 arestas e de cada um dos vértices restantes , 3 arestas . Qual o número de
vértices do poliedro ?
8) Um poliedro convexo possui apenas faces triangulares e quadrangulares . Sabendo que o
número de faces triangulares e quadrangulares são diretamente proporcionais aos números 2 e 3
e que o número de arestas é o dobro do número de vértices , calcule o número total de faces
desse poliedro .
b) V = 11, A = 17, F = 8 e S = 3.240º
6) F = 9
7) V = 21
8) F = 10
9) A=19 e V = 10
10) D
- Tetraedros Regulares Questões
Artigo sobre tetraedros, área e volume dos tetraedros com questões resolvidas e propostas. O tetraedro regular é um sólido platônico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros (triângulos...
- Cubo E Paralelepípedo Questões Vestibular
Questões de vestibular sobre cubo e paralelepípedo 1) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4? d² = 2² + 2² d² = 8 d = 2?22) Se um cubo tem suas arestas aumentadas em...
- Pirâmides Questões Vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos. Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
Vestibular
Poliedros questões vestibular
Artigo com questões de vestibular sobre poliedros resolvidas e propostas
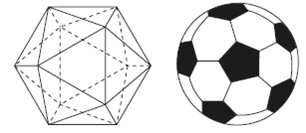
1) Arquimedes descobriu um poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais, todas regulares. Esse poliedro inspirou a fabricação da bola de futebol que apareceu pela primeira vez na Copa do Mundo de 1970. Quantos vértices possui esse poliedro?

Resolução:
Como o poliedro tem 12 faces pentagonais, então:
12 . 5 = 60
O poliedro tem 20 faces hexagonais, assim 20 . 6 = 120, logo: F = 12 + 20 = 32
Cada aresta foi contada duas vezes, portanto temos:
2A = 60 + 120
A = 90
A = 90
Como o poliedro é convexo, vale a relação de Euler,
V ? A + F = 2, portanto:
V ? 90 + 32 =2
V = 2 + 90 ? 32
V = 60
V = 2 + 90 ? 32
V = 60
Assim, o número de vértices é 60.
2) Determinar o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.
Resolução:
Como o poliedro tem 6 faces quadrangulares, calculamos: 6 . 4 = 24
O poliedro tem 4 faces triangulares: 4 . 3 = 12
Como cada aresta foi contada duas vezes, o número total de arestas é: A = (24+12)/2 = 18
Temos então F = 10, A = 18.
Aplicando a relação de Euler:
V ? A + F = 2
V ? 18 + 10 = 2
V = 10
V ? 18 + 10 = 2
V = 10
Logo, o poliedro tem 18 arestas e 10 vértices.
3) (FAAP - SP) Num poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Calcule o número de faces.
Essa é a Relação de Euler para poliedros convexos: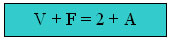 |
De acordo com o enunciado, temos:
A = V + 6
Usando a Relação de Euler e substituindo A de acordo com a igualdade acima:
V + F = 2 + A
V + F = 2 + V + 6
Eliminando V:
F = 8
O número de faces é igual a 8.
4) (Fatec - SP) Um poliedro convexo tem 3 faces com 4 lados, 2 faces com 3 lados e 4 faces com 5 lados. Qual é o número de vértices desse poliedro?
Resolução:
Do enunciado, sabemos que
Número de faces: 3 + 2 + 4 = 9
Número de arestas:
3 faces com 4 lados: 3 . 4 = 12
2 faces com 3 lados: 2 . 3 = 6
4 faces com 5 lados: 4 . 5 = 20
Somando: 12 + 6 + 20 = 38
Atenção: as faces são unidas, duas a duas, por uma aresta. Ao contarmos todas as arestas de todas as faces, cada aresta é contada duas vezes, uma para cada face "grudada" nela. Assim, esse número, na verdade, é o dobro do número real de arestas do poliedro. Logo:
A = 38 ÷ 2 = 19.
Usando, agora, a Relação de Euler, temos:
V + F = 2 + A
V + 9 = 2 + 19
V = 21 - 9 = 12.
A = V + 6
Usando a Relação de Euler e substituindo A de acordo com a igualdade acima:
V + F = 2 + A
V + F = 2 + V + 6
Eliminando V:
F = 8
O número de faces é igual a 8.
4) (Fatec - SP) Um poliedro convexo tem 3 faces com 4 lados, 2 faces com 3 lados e 4 faces com 5 lados. Qual é o número de vértices desse poliedro?
Resolução:
Do enunciado, sabemos que
Número de faces: 3 + 2 + 4 = 9
Número de arestas:
3 faces com 4 lados: 3 . 4 = 12
2 faces com 3 lados: 2 . 3 = 6
4 faces com 5 lados: 4 . 5 = 20
Somando: 12 + 6 + 20 = 38
Atenção: as faces são unidas, duas a duas, por uma aresta. Ao contarmos todas as arestas de todas as faces, cada aresta é contada duas vezes, uma para cada face "grudada" nela. Assim, esse número, na verdade, é o dobro do número real de arestas do poliedro. Logo:
A = 38 ÷ 2 = 19.
Usando, agora, a Relação de Euler, temos:
V + F = 2 + A
V + 9 = 2 + 19
V = 21 - 9 = 12.
5) Determine o número de vértices, arestas, faces e a soma dos ângulos das faces dos poliedros convexo que possuem:
a) 6 faces triangulares e 4 faces quadrangulares.
b) 5 faces pentagonais 3 faces triangulares.
6) Um poliedro convexo apresenta faces quadrangulares e triangulares . Calcule o número de
faces desse poliedro , sabendo-se que o número de arestas é o quádruplo do número de faces
triangulares e o número de faces quadrangulares é igual a 5 .
vértices partem 4 arestas e de cada um dos vértices restantes , 3 arestas . Qual o número de
vértices do poliedro ?
8) Um poliedro convexo possui apenas faces triangulares e quadrangulares . Sabendo que o
número de faces triangulares e quadrangulares são diretamente proporcionais aos números 2 e 3
e que o número de arestas é o dobro do número de vértices , calcule o número total de faces
desse poliedro .
9) Um poliedro convexo de onze faces , tem seis faces triangulares e cinco faces
quadrangulares . Calcular o número de arestas e de vértices do poliedro.
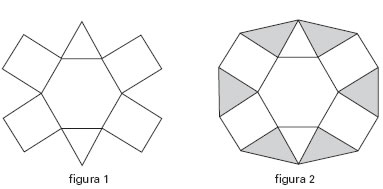
10) (UFSCAR) A figura 1 representa um determinado encaixe no plano de 7 ladrilhos poligonais regulares (1 hexágono, 2 triângulos, 4 quadrados), sem sobreposições e cortes.

Em relação aos 6 ladrilhos triangulares colocados perfeitamente nos espaços da figura 1, como indicado na figura 2, é correto dizer que
A) 2 são triângulos equiláteros e 4 são triângulos isósceles de ângulo da base medindo 15°.
B) 2 são triângulos equiláteros e 4 são triângulos isósceles de ângulo da base medindo 30°.
C) 2 são triângulos isósceles de ângulo da base medindo 50° e 4 são triângulos isósceles de ângulo da base medindo 30°.
D) 2 são triângulos equiláteros e 4 são triângulos retângulos isósceles.
E) 2 são triângulos equiláteros e 4 são triângulos escalenos.
A) 2 são triângulos equiláteros e 4 são triângulos isósceles de ângulo da base medindo 15°.
B) 2 são triângulos equiláteros e 4 são triângulos isósceles de ângulo da base medindo 30°.
C) 2 são triângulos isósceles de ângulo da base medindo 50° e 4 são triângulos isósceles de ângulo da base medindo 30°.
D) 2 são triângulos equiláteros e 4 são triângulos retângulos isósceles.
E) 2 são triângulos equiláteros e 4 são triângulos escalenos.
11) Obter o número de arestas de um poliedro convexo que tem 6 faces e 8 vértices.
12) Quantos vértices tem um poliedro convexo com 4 faces triangulares e 5 faces quadrangulares?
Gabarito:
5) a) V = 9, A = 17, F = 10 e S = 2.520ºb) V = 11, A = 17, F = 8 e S = 3.240º
6) F = 9
7) V = 21
8) F = 10
9) A=19 e V = 10
10) D
11) A = 12
12) V = 9
- Tetraedros Regulares Questões
Artigo sobre tetraedros, área e volume dos tetraedros com questões resolvidas e propostas. O tetraedro regular é um sólido platônico representante do elemento fogo, figura geométrica espacial formada por quatro triângulos equiláteros (triângulos...
- Cubo E Paralelepípedo Questões Vestibular
Questões de vestibular sobre cubo e paralelepípedo 1) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4? d² = 2² + 2² d² = 8 d = 2?22) Se um cubo tem suas arestas aumentadas em...
- Pirâmides Questões Vestibular
Artigo sobre pirâmides, classificação das pirâmides, área e volume das pirâmides e questões de vestibular propostos e resolvidos. Uma pirâmide é um poliedro, cuja base é um polígono qualquer e cujas faces laterais são triângulos com um vértice...
- área E Volume Dos Prismas Fórmulas
Artigo sobre área e volume dos prisma fórmulas e exemplos. Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas...
- ângulos Poliédricos Questões
Ângulos poliédricos são os formados entre dois planos de um diedro, triedro ou poliedro. Sejam n semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em...
