Vestibular
Frequência e Período de um Movimento Circular Uniforme (MCU)
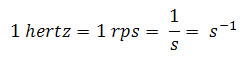
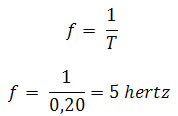
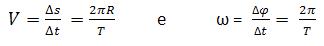
Equação da velocidade linear e trajetória realizada por um móvel qualquer
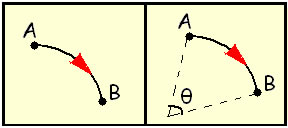
Análise do movimento curvilíneo
É importante observar que quando a velocidade do móvel ocorre de forma curva, é necessário analisar, além da velocidade linear, um outro tipo de velocidade presente: a velocidade angular, que é exatamente o ângulo ?, formado imaginariamente entre a ligação dos pontos da trajetória.
A representação matemática do cálculo da velocidade angular é dada pela equação: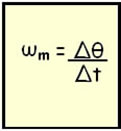
Exemplo:
 = V/R = 30,0/100
= V/R = 30,0/100 = 0,3 rad / s
= 0,3 rad / s
A junção dessas duas velocidades (linear e curvilínea) proporciona o nascimento de uma nova equação para se calcular o movimento circular.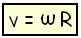
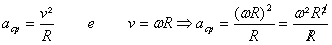
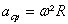
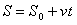
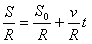
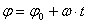 Exemplo:
Exemplo:
Espaço Angular (?)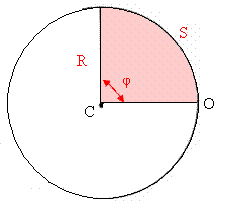
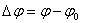
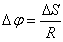
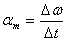
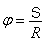
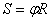
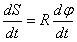
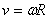
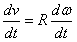
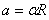
 Num MCU a velocidade angular (W) e a escalar (V) são sempre as mesmas em qualquer intervalo de tempo. Dividindo todos os termos da equação horária do movimento uniforme (S=So + V.t) pelo raio R da trajetória: S/R= So/R + Vt/R --- S/R=? ---
Num MCU a velocidade angular (W) e a escalar (V) são sempre as mesmas em qualquer intervalo de tempo. Dividindo todos os termos da equação horária do movimento uniforme (S=So + V.t) pelo raio R da trajetória: S/R= So/R + Vt/R --- S/R=? --- 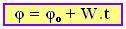
. .
Movimento Circular Uniformemente Variado
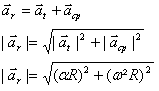
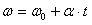
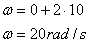
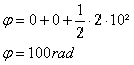
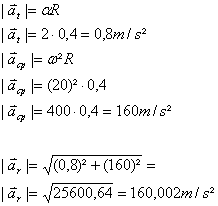
Fontes: www.sofisica.com.br/
4) Um motor executa 600 rpm. Determine a freqüência e o período no SI.
5) Um ponto material em MCU, numa circunferência horizontal, completa uma volta a cada 10 s. Sabendo-se que o raio da circunferência é 5 cm.
a) a Lua não efetua rotação e nem translação.
b) a Lua não efetua rotação, apenas translação.
c) os períodos de rotação e translação da Lua são iguais.
d) as oportunidades para se observar a face oculta coincidem com o período diurno da Terra.
e) enquanto a Lua dá uma volta em torno da Terra, esta dá uma volta em torno do seu eixo.
22)
a) O valor da:
a.1) Posição angular inicial;
- Leis De Kepler - Resumo (com Questões)
Primeira Lei de Kepler (Lei das órbitas) Primeira Lei de Kepler é a lei das órbitas, que diz:?? Todos os planetas se movem em orbitas elípticas tendo o Sol como um dos focos?? (HALLIDAY, David, Física 2, pg. 14.)...
- Vetores - Resumo (com Questões)
Grandezas escalares e vetoriaisAlgumas grandezas físicas exigem, para sua perfeita caracterização, apenas uma intensidade. Essas grandezas são denominadas grandezas escalares. Assim, grandezas físicas, como massa, comprimento, tempo,...
- Movimento Uniforme (mu) E Movimento Uniformemente Variado (muv) - Resumo (com Questões)
Definição de movimento uniforme A tartaruga é um bicho estranho. Pode o mundo cair ao seu redor que ela continua se movimentando sem alterar a sua velocidade. Depois que ela sai do repouso e entra em movimento, ela dificilmente varia sua velocidade...
- Velocidade Escalar Média E Deslocamento Escalar: Exemplos E Questões Resolvidas
Artigo sobre velocidade escalar média, trajetória, intervalo de tempo e deslocamento com questões resolvidas. Velocidade escalar média A velocidade escalar média é a relação entre o deslocamento escalar ?s e o correspondente intervalo...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...
Vestibular
Movimento circular uniforme e uniformemente variado - Definição e fórmulas (com questões)
Movimento Circular Uniforme (MCU)
Um corpo está em Movimento Curvilíneo Uniforme, se sua trajetória for descrita por um círculo com um "eixo de rotação" a uma distância R, e sua velocidade for constante, ou seja, a mesma em todos os pontos do percurso.
No cotidiano, observamos muitos exemplos de MCU, como uma roda gigante, um carrossel ou as pás de um ventilador girando.
O movimento circular uniforme é um movimento periódico porque é um movimento que se repete em intervalos de tempos iguais: o móvel passa repetidas vezes pela mesma posição e nas mesmas condições (mesma velocidade e aceleração)
Frequência e Período de um Movimento Circular Uniforme (MCU)
Vamos imaginar que uma partícula descreva um movimento circular uniforme. Nesse caso, o tempo que corresponde a uma volta é sempre igual, passando a ser chamado de período do movimento. O período é representado por T. A frequência (f) desse movimento está relacionada diretamente ao número de voltas por unidade de tempo. Assim, temos:
f = N
?t
?t
Onde N é o número de voltas efetuadas no intervalo de tempo ?t. Observe que a frequência coincidirá com a velocidade angular (?) quando a unidade de ângulo for revolução.
A frequência pode ser dada em revoluções por hora (rph), revoluções por minuto (rpm), revoluções por segundo (rps), etc. No Sistema Internacional, a unidade de frequência é o hertz (Hz), que é igual a 1 revolução por segundo:
1 Hz = 1 hertz = 1 rps = 1 revolução por segundo
Se na equação acima fizermos N = 1, o intervalo de tempo ?t deverá ser igual a um período (T):
A frequência pode ser dada em revoluções por hora (rph), revoluções por minuto (rpm), revoluções por segundo (rps), etc. No Sistema Internacional, a unidade de frequência é o hertz (Hz), que é igual a 1 revolução por segundo:
1 Hz = 1 hertz = 1 rps = 1 revolução por segundo
Se na equação acima fizermos N = 1, o intervalo de tempo ?t deverá ser igual a um período (T):
f = 1
T
T
A unidade de ângulo é adimensional, dessa forma, na unidade de frequência podemos omitir a palavra revolução.
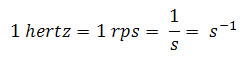
Vejamos o exemplo abaixo:
Suponhamos que um corpo tenha movimento de rotação uniforme de período T = 0,20 s. Calcule a frequência do movimento em hertz.
Solução:
Suponhamos que um corpo tenha movimento de rotação uniforme de período T = 0,20 s. Calcule a frequência do movimento em hertz.
Solução:
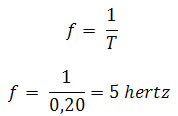
Velocidades no Movimento Circular Uniforme
Velocidades escalares no movimento circular e uniforme
Sempre no movimento circular uniforme, as velocidades escalares e lineares serão constantes, e com isso, seus valores médios e instantâneos irão coincidir.
É importante ressaltar que para o móvel realizar uma volta completa em uma trajetória circular de raio R, seu deslocamento será de 2?R, seu ângulo descrito será de 2? rad, e seu tempo gasto é representado pelo período T. Vejamos:
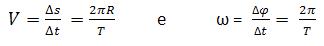
Não podemos esquecer que a frequência é o contrário do período, e portanto, temos:
V = 2? f R
e
? = 2? f
e
? = 2? f
Velocidade Angular (?) de movimento Circular Uniforme
A velocidade de um móvel constante e linear é representada pela equação a seguir, que indica a trajetória realizada pelo móvel.

Equação da velocidade linear e trajetória realizada por um móvel qualquer
Agora, quando a velocidade do móvel ocorre de forma curvilínea (curva) ou circular teremos a análise da velocidade angular.

Análise do movimento curvilíneo
É importante observar que quando a velocidade do móvel ocorre de forma curva, é necessário analisar, além da velocidade linear, um outro tipo de velocidade presente: a velocidade angular, que é exatamente o ângulo ?, formado imaginariamente entre a ligação dos pontos da trajetória.
A representação matemática do cálculo da velocidade angular é dada pela equação:
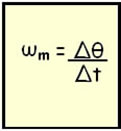
Onde:
?m = velocidade angular do móvel
?? = deslocamento do móvel
?t = tempo
Podemos concluir, então, que a velocidade angular do movimento circular uniforme é a relação existente entre o ângulo da trajetória descrito e o tempo gasto para se concluir essa descrição.
?m = velocidade angular do móvel
?? = deslocamento do móvel
?t = tempo
Podemos concluir, então, que a velocidade angular do movimento circular uniforme é a relação existente entre o ângulo da trajetória descrito e o tempo gasto para se concluir essa descrição.
A unidade de velocidade angular no Sistema Internacional é: rad / s.
OBS : 2p radianos = 6,28 radianos = 360o
p radianos = 3,14 radianos = 180o
1 radiano = 57,3o ( aprox. )
p radianos = 3,14 radianos = 180o
1 radiano = 57,3o ( aprox. )
Exemplo:
Um carro com a velocidade escalar constante de 30,0 m/s faz uma trajetória circular de raio 100 m. Determinar a velocidade angular.
Dados: V = 30,0 m/s e R = 100 m
Temos que:
 = V/R = 30,0/100
= V/R = 30,0/100 = 0,3 rad / s
= 0,3 rad / sA junção dessas duas velocidades (linear e curvilínea) proporciona o nascimento de uma nova equação para se calcular o movimento circular.
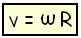
Onde:
v = velocidade linear
? = velocidade angular
R = raio
Relação entre a velocidade escalar e a velocidade angular:
Vimos que: v = 2p Rf e w = 2pf então:
| V = w. R |
Aceleração Centrípeta
Você pode estar achando estranho falarmos sobre a aceleração em uma aula de movimento uniforme. Afinal, nesse movimento a velocidade é constante e a aceleração é uma grandeza ligada à variação de velocidade.
Para entender onde a aceleração se encaixa aqui, primeiro precisamos ampliar a nossa visão sobre o que é a variação de velocidade. Estamos acostumados a entendê-la como sendo uma variação na sua intensidade, mas não é só isso. A velocidade pode variar na sua direção e sentido e, para isso, também é necessária uma aceleração.
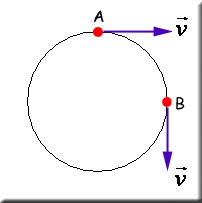
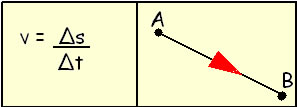
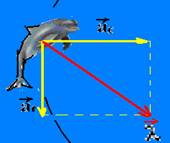
Quando falamos de movimento circular, é importante perceber que a direção da velocidade está mudando durante a realização da curva, como pode ser ilustrado na figura a seguir, que representa um movimento de um objeto de um ponto A para um ponto B, realizando um quarto de volta.
Para entender onde a aceleração se encaixa aqui, primeiro precisamos ampliar a nossa visão sobre o que é a variação de velocidade. Estamos acostumados a entendê-la como sendo uma variação na sua intensidade, mas não é só isso. A velocidade pode variar na sua direção e sentido e, para isso, também é necessária uma aceleração.
Quando falamos de movimento circular, é importante perceber que a direção da velocidade está mudando durante a realização da curva, como pode ser ilustrado na figura a seguir, que representa um movimento de um objeto de um ponto A para um ponto B, realizando um quarto de volta.
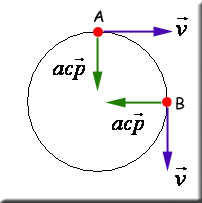
Observe que no inicio da curva (ponto A) a velocidade é horizontal e para a direita e depois de um quarto de volta, ponto B, a velocidade é vertical e para baixo. Apesar de a velocidade ser constante, deve existir uma aceleração para variar a direção da velocidade. Essa aceleração é chamada de aceleração centrípeta (acp) e, como diz o nome, ela sempre está direcionada para o centro da curva.
Observe que a aceleração centrípeta faz noventa graus com a velocidade. É por isso que ela provoca a variação na direção do vetor velocidade. A intensidade da aceleração centrípeta e dada pela expressão a seguir:
| Aceleração Centrípeta |
| Onde R é o raio da curva |
Esta aceleração é relacionada com a velocidade angular da seguinte forma:
Sabendo que 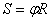 e que
e que 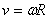 , pode-se converter a função horária do espaço linear para o espaço angular:
, pode-se converter a função horária do espaço linear para o espaço angular:
então:
Vamos determinar o valor da aceleração centrípeta, sabendo que o carro faz a trajetória circular com uma velocidade escalar constante igual 20,0 m/s e o raio da trajetória é igual a 100 m.
Dados: V = 20,0 m/s e R = 100 m
De (5.1) temos que:
ac = V2/R
Substituindo os valores de V e R, obtemos:
ac = 20,02/100 = 400/100
| ac = 4,0 m/s2 |
Transmissão de movimento circular
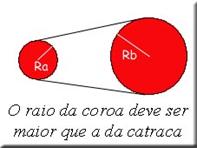
Para entendermos o conceito de transmissão de movimento circular, vamos usar como exemplo um meio de transporte muito conhecido. Quando se pedala uma bicicleta, executa-se um movimento circular em uma roda dentada (coroa) através dos pedais. Esse movimento é transmitindo através de uma corrente para outra roda dentada de menor raio, a catraca, que está ligada à roda traseira da bicicleta. É fácil observar que a bicicleta se move com uma velocidade maior que aquela com que se está pedalando, e isso ocorre devido à diferença dos raios entre a coroa e a catraca.
Na transmissão de movimento circular apresentada, a velocidade linear é a mesma para a coroa e a catraca e por isso vale a seguinte relação entre raios e frequência de rotação.
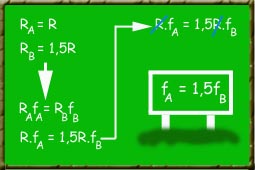
Para entender como funciona o mecanismo da equação acima, vamos considerar uma bicicleta que tem uma coroa com um raio uma vez e meia maior que o raio da catraca. Se aplicarmos esses dados na equação acima, veremos que a frequência da catraca será uma vez e meia maior que a da coroa. Tal procedimento é detalhado no quadro seguinte.
O resultado acima mostra que, quando se dá uma volta com a coroa, a catraca fará uma volta e meia. É por isso bicicleta tem se desloca a uma velocidade maior que a velocidade com que se está pedalando.
Grandezas Angulares
As grandezas até agora utilizadas de deslocamento/espaço (s, h, x, y), de velocidade (v) e de aceleração (a), eram úteis quando o objetivo era descrever movimentos lineares, mas na análise de movimentos circulares, devemos introduzir novas grandezas, que são chamadas grandezas angulares, medidas sempre em radianos. São elas:
- deslocamento/espaço angular: ? (phi)
- velocidade angular: ? (ômega)
- aceleração angular: ? (alpha)
| Saiba mais... Da definição de radiano temos: Desta definição é possível obter a relação: E também é possível saber que o arco correspondente a 1rad é o ângulo formado quando seu arco S tem o mesmo comprimento do raio R. |
Espaço Angular (?)
Chama-se espaço angular o espaço do arco formado, quando um móvel encontra-se a uma abertura de ângulo ? qualquer em relação ao ponto denominado origem.
E é calculado por: 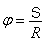
Deslocamento angular (??)
Assim como para o deslocamento linear, temos um deslocamento angular se calcularmos a diferença entre a posição angular final e a posição angular inicial:
Sendo:
Por convenção:
No sentido anti-horário o deslocamento angular é positivo.
No sentido horário o deslocamento angular é negativo.
Aceleração Angular (?)
Seguindo a mesma analogia utilizada para a velocidade angular, definimos aceleração angular média como:
Algumas relações importantes
Através da definição de radiano dada anteriormente temos que:
mas se isolarmos S:
derivando esta igualdade em ambos os lados em função do tempo obteremos:
mas a derivada da Posição em função do tempo é igual a velocidade linear e a derivada da Posição Angular em função do tempo é igual a velocidade angular, logo:
onde podemos novamente derivar a igualdade em função do tempo e obteremos:
mas a derivada da velocidade linear em função do tempo é igual a aceleração linear, que no movimento circular é tangente à trajetória, e a derivada da velocidade angular em função do tempo é igual a aceleração angular, então:
Então:
Linear | Angular | |
S | = | ?R |
v | = | ?R |
a | = | ?R |
Função horária do Movimento Circular Uniforme (MCU)
 Num MCU a velocidade angular (W) e a escalar (V) são sempre as mesmas em qualquer intervalo de tempo. Dividindo todos os termos da equação horária do movimento uniforme (S=So + V.t) pelo raio R da trajetória: S/R= So/R + Vt/R --- S/R=? ---
Num MCU a velocidade angular (W) e a escalar (V) são sempre as mesmas em qualquer intervalo de tempo. Dividindo todos os termos da equação horária do movimento uniforme (S=So + V.t) pelo raio R da trajetória: S/R= So/R + Vt/R --- S/R=? --- So/R=?o --- V/R=W --- ? = ?o + W.t
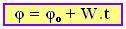
A equação acima recebe o nome de equação (função) horária do MCU na forma angular, e aos termos ? e ?o dá-se o nome de fases (ou ângulos) final e inicial, respectivamente.
RESUMO DE FÓRMULAS DO MOVIMENTO CIRCULAR UNIFORME
Equações básicas do movimento circular uniforme (resumo)
.
| Descrição | Equações |
| Equação linear da posição | s = so + v.t |
| Equação angular da posição | ? = ?o + ?.t |
| Aceleração centrípeta | v² acp = ? R |
| Velocidade linear | 2?R v = ?? T |
| Velocidade angular | 2? ? = ?? T |
| Relação entre V e ? | v ? = ?? R |
| Frequência | 1 n f = ? = ?? T ?t |
Quando um corpo, que descreve trajetória circular, e sofre mudança na sua velocidade angular, então este corpo tem aceleração angular (?).
As formas angulares das equações do Movimento Curvilíneo Uniformemente Variado são obtidas quando divididas pelo raio R da trajetória a que se movimenta o corpo.
Assim:
MUV | MCUV | |
Grandezas lineares | Grandezas angulares | |
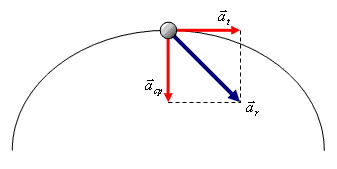
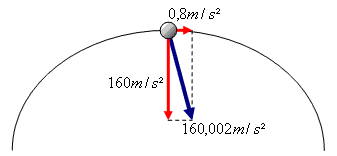
E, aceleração resultante é dada pela soma vetorial da aceleração tangencial e da aceleração centípeta:
Exemplo:
Um volante circular como raio 0,4 metros gira, partindo do repouso, com aceleração angular igual a 2rad/s².
(a) Qual será a sua velocidade angular depois de 10 segundos?
(b) Qual será o ângulo descrito neste tempo?
(c) Qual será o vetor aceleração resultante?
(a) Pela função horária da velocidade angular:
(b) Pela função horária do deslocamento angular:
(c) Pelas relações estabelecidas de aceleração tangencial e centrípeta:
Fontes: www.sofisica.com.br/
www.brasilescola.com/
fisicashow.blogspot.com.br/
www.alunosonline.com.br/
educacao.uol.com.br/
fisicashow.blogspot.com.br/
www.alunosonline.com.br/
educacao.uol.com.br/
Questões resolvidas sobre Movimento Circular e Movimento Circular Uniformemente Variado
1) A velocidade angular de um móvel em trajetória circular é diminuída de 30.? rad/s para 20. ? rad/s em um intervalo de tempo igual à 2 s. Sabendo que o raio do círculo mede 0,5 m e o movimento é uniformemente variado; determine a aceleração escalar deste móvel.
2) (UNESP) Um ?motorzinho? de dentista gira com frequência de 2000 Hz até a broca de raio 2,0 mm encostar no dente do paciente, quando, após 1,5 s, passa a ter frequência de 500 Hz. Determine o módulo da aceleração escalar média neste intervalo de tempo.
3) Um disco efetua 30 voltas em um minuto. Determine a freqüência em Hz e rpm.
5) Um ponto material em MCU, numa circunferência horizontal, completa uma volta a cada 10 s. Sabendo-se que o raio da circunferência é 5 cm.
Calcule:
a) o período e a freqüência;
b) a velocidade angular;
c) a velocidade escalar;
d) o módulo da aceleração centrípeta.
6) (UFGO) Uma partícula executa um movimento circular uniforme de raio 1 m com aceleração 0,25 m/s². O período do movimento é:
a) 2?
b) 4?
c) 8?
d) ?/2
e) ?/4
7) (PUC-MG) A roda de um carro tem diâmetro de 60 cm e efetua 150 rotações por minuto (150 rpm). A distância percorrida pelo carro em 10 s será, em centímetros, de:
a) 2000?
b) 3000 ?
c) 1.800?
d) 1.500?
8) (FATEC-SP) Uma formiga, encontrando-se no centro de uma roda-gigante que gira uniformemente, caminha para um carrinho. Á medida que a formiga se aproxima do carrinho:
a) seu período aumenta.
b) sua frequência aumenta.
c) sua velocidade angular cresce.
d) sua velocidade angular aumenta.
e) sua aceleração escalar diminui.
9) Considere duas pessoas, ambas na superfície da Terra, uma na linha do Equador e a outra sobre o Trópico de Capricórnio. Considere, ainda, somente o movimento de rotação da Terra em torno de seu eixo. Com base nessas informações, compare para as duas pessoas:
a) as velocidades angulares;
b) as frequências;
c) os módulos das velocidades lineares;
d) os módulos das acelerações centrípetas.
a) o período e a freqüência;
b) a velocidade angular;
c) a velocidade escalar;
d) o módulo da aceleração centrípeta.
6) (UFGO) Uma partícula executa um movimento circular uniforme de raio 1 m com aceleração 0,25 m/s². O período do movimento é:
a) 2?
b) 4?
c) 8?
d) ?/2
e) ?/4
7) (PUC-MG) A roda de um carro tem diâmetro de 60 cm e efetua 150 rotações por minuto (150 rpm). A distância percorrida pelo carro em 10 s será, em centímetros, de:
a) 2000?
b) 3000 ?
c) 1.800?
d) 1.500?
8) (FATEC-SP) Uma formiga, encontrando-se no centro de uma roda-gigante que gira uniformemente, caminha para um carrinho. Á medida que a formiga se aproxima do carrinho:
a) seu período aumenta.
b) sua frequência aumenta.
c) sua velocidade angular cresce.
d) sua velocidade angular aumenta.
e) sua aceleração escalar diminui.
9) Considere duas pessoas, ambas na superfície da Terra, uma na linha do Equador e a outra sobre o Trópico de Capricórnio. Considere, ainda, somente o movimento de rotação da Terra em torno de seu eixo. Com base nessas informações, compare para as duas pessoas:
a) as velocidades angulares;
b) as frequências;
c) os módulos das velocidades lineares;
d) os módulos das acelerações centrípetas.
10) (UFB) Um pêndulo oscila de um ponto extremo A a outro ponto extremo B, em 3 s.
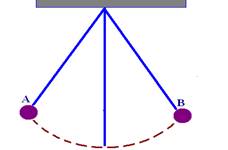



Determine:
a) O período de encontros na posição P.
b) O período de encontros.


a) 0,50 s, 2,0 Hz e (p/2) rad/s
b) 2,0 s, 0,50 Hz e p rad/s
c) 2,0 s, 1,0 Hz e 2p rad/s
d) 0,50 s, 2,0 Hz e p rad/s
e) 2,0 s, 2,0 Hz e 2p rad/s

Qual é o seu período e sua freqüência?
11) (PUC-SP-011) Lucas foi presenteado com um ventilador que, 20 s após ser ligado, atinge uma frequência de 300 rpm em um

movimento uniformemente acelerado. O espírito científico de Lucas o fez se perguntar qual seria o
número de voltas efetuadas pelas pás do ventilador durante esse intervalo de tempo. Usando seus
conhecimentos de Física, ele encontrou
a) 300 voltas b) 900 voltas c) 18000 voltas d) 50 voltas e) 6000 voltas
12) -(UERJ-RJ-09) Dois móveis, A e B, percorrem uma pista circular em movimento uniforme.

Os dois móveis partiram do mesmo ponto e no mesmo sentido com as velocidades de 1,5 rad/s e 3,0 rad/s, respectivamente; o móvel B, porém, partiu 4 segundos após o A.
Calcule o intervalo de tempo decorrido, após a partida de A, no qual o móvel B alcançou o móvel A pela primeira vez.
13) (FATEC-SP) Em um estádio esportivo, uma pista circular tem raio igual a 12,0 m. Dois atletas A e B percorrem a pista no mesmo sentido com velocidades constantes VA = 8 m/s e VB = 6m/s. Ambos passam por um mesmo ponto na data zero.

O corredor mais veloz estará com uma volta de vantagem sobre o outro na data: (considere ?=3)
a) 35 s b) 15 s c) 20 s d) 60 s e) 36,0 s
14) (UNICAMP) - Dois moveis A e B percorrem uma mesma circunferência com movimentos uniformes, em sentidos opostos.

O móvel A tem período de 6 s e o móvel B, 12 s. No instante to = 0 os moveis passam pela mesma posição P.
Determine:
a) O período de encontros na posição P.
b) O período de encontros.
15) (FMS-SP) Sobre uma circunferência com 60 cm de raio, dois pontos animados de movimento uniforme se encontram a cada 30 s quando se movem no mesmo sentido e a cada 10s quando se movem em sentidos opostos. Determine seus períodos.
16) (PUC-RS) A freqüência e o período dos minutos de um relógio são, respectivamente:

a) (1/3.600) Hz e 3.600 s b) (1/60) Hz e 3.600 s
c) (1/60) Hz e 60 min d) 60 Hz e 60 s e) 60 Hz e (1/60) min
17) (UFB) Um ponto material realiza um MCU de raio R=4 m, obedecendo à função horária angular ? = ?/4 + ?/2.t (rad;s). Determine:
a) o ângulo (fase) inicial do movimento
b) a velocidade angular do movimento
c) o ângulo de fase após 8 s de movimento e o número de voltas completas que ele efetuou nesse tempo
d) a função horária na forma escalar (linear)
18) (PUC-SP) Um corpo parte do repouso e percorre uma trajetória circular de raio 1 m, assumindo movimento uniformemente retardado de aceleração escalar 1 m/s2.

Esquematize as acelerações e calcule suas intensidades no instante t=2s.
19) (UFJF-MG) No ato de manobrar seu carro para estacionar, uma motorista deixa um dos pneus raspar no meio fio. Com isso, uma pequena mancha branca fica no pneu. À noite, o carro está passando em frente a uma casa noturna iluminada por uma lâmpada estroboscópica com freqüência de 5Hz. Nessa situação, uma pessoa olha e tem a impressão de que o pneu com a mancha branca está girando como se o carro estivesse se movendo para trás, embora ele esteja deslocando-se para frente. Uma possível razão para isto é que a freqüência de rotação do pneu é:
a) maior que 5 Hz e menor que 6 Hz.
b) maior que 4 Hz e menor que 5 Hz.
c) exatamente igual a 5 Hz.
d) maior que 10 Hz e menor que 11 Hz.
e) certamente maior que 5 Hz.
20) (U. Mogi das Cruzes-SP) Um ponto material possui movimento circular uniforme e realiza uma volta a cada 2,0 s. O período, a freqüência e a velocidade angular desse móvel são, respectivamente:
b) 2,0 s, 0,50 Hz e p rad/s
c) 2,0 s, 1,0 Hz e 2p rad/s
d) 0,50 s, 2,0 Hz e p rad/s
e) 2,0 s, 2,0 Hz e 2p rad/s
21) (Vunesp-SP) Quem está na Terra vê sempre a mesma face da lua. Isto ocorre porque:
a) a Lua não efetua rotação e nem translação.
b) a Lua não efetua rotação, apenas translação.
c) os períodos de rotação e translação da Lua são iguais.
d) as oportunidades para se observar a face oculta coincidem com o período diurno da Terra.
e) enquanto a Lua dá uma volta em torno da Terra, esta dá uma volta em torno do seu eixo.
22)
a) possuem a mesma velocidade angular.
b) a aceleração angular do segundo ponteiro é maior.
c) possuem a mesma freqüência.
d) o período do primeiro é maior.
e) a velocidade angular do primeiro é maior.
23) Uma partícula, que executa 150 rpm (rotações por minutos), descreve no sentido horário, uma trajetória circular de raio 20 cm.
a) Determine para o movimento da partícula:
a.1) O Período.
a.2) A velocidade linear.
a.3) A velocidade angular.
a.4) A aceleração centrípeta.
b) Para o instante de tempo de 0,30 s, calcule:
b.1) O comprimento do arco descrito pela partícula (variação do espaço).
b.2) O ângulo ao centro descrito pela partícula (variação do ângulo).
24) Uma partícula descreve uma circunferência de raio 2 m. A posição angular da partícula é dada por: ?=4-2t+2t2. Determine:
a) O valor da:
a.1) Posição angular inicial;
a.2) Velocidade angular inicial;
a.3) Aceleração angular da partícula.
25) (FAAP) Dois pontos A e B situam-se respectivamente a 10 cm e 20 cm do eixo de rotação da roda de um automóvel em movimento uniforme. É possível afirmar que:
a)10 e 0,002
b) 30 e 0,002
c) 30 e 0,006
d) 20 e 0,006
e) 10 e 0,006
30) (UDESC 2008) A maior roda gigante do mundo em funcionamento, chamada Estrela de Nachang, fica localizada na China e tem 160 m de altura. Em fevereiro de 2008 começará a funcionar o Observador de Singapura , com 165 m de altura e 150 m de diâmetro, que, movendo-se com velocidade constante, leva aproximadamente 40,0 minutos para completar uma volta. A distância percorrida pelas cabines do Observador de Singapura, após completar uma volta, e sua velocidade angular média são, respectivamente, iguais a:
a) 165 ? m; 0,157 rad/min.
b) 165 ? m; 40 rad/min.
c) 160 ? m; 0,157 rad/min.
d) 150 ? m; 0,157 rad/min.
e) 150 ? m; 40 rad/min.
a) O período do movimento de A é menor que o de B.
b) A freqüência do movimento de A é maior que a de B.
c) A velocidade angular do movimento de B é maior que a de A.
b) A freqüência do movimento de A é maior que a de B.
c) A velocidade angular do movimento de B é maior que a de A.
d) As velocidades angulares de A e B são iguais.
e) As velocidades lineares de A e B têm mesma intensidade.
26) (CEFET-PR) A órbita da Terra em torno do Sol, em razão da sua baixa excentricidade, é aproximadamente uma circunferência. Sabendo-se que a terra leva um ano para realizar uma volta completa em torno do Sol e que a distância média da Terra ao Sol é 150 milhões de Km, os módulos dos vetores da velocidade e aceleração em km/s e m/s² são respectivamente: *
a)10 e 0,002
b) 30 e 0,002
c) 30 e 0,006
d) 20 e 0,006
e) 10 e 0,006
27) (ITA) Um automóvel percorre uma trajetória com velocidade escalar constante. A roda do automóvel, cujo raio é 30 cm, dá 40 voltas em 2,0 s. A Velocidade escalar angular da roda é, em rad/s: *
a)20?
b) 30?
c) 40?
d) 50?
e) 60?
28) (UFES) Uma pessoa está em uma roda-gigante que tem raio de 5m e gira em rotação uniforme. A pessoa passa pelo ponto mais próximo do chão a cada 20 segundos. Podemos afirmar que a frequência do movimento dessa pessoa, em rpm, é: *
a) 1
b) 2
c) 3
d) 4
e) 5
29) (FCC) Uma partícula executa um movimento uniforme sobre uma circunferência de raio 20 cm. Ela percorre metade da circunferência em 2,0 s. A frequência, em hertz, e o período do movimento, em segundos, valem, respectivamente : *
a) 4,0 e 0,25
b) 1,0 e 1,0
c) 0,25 e 4,0
d) 2,0 e 0,5
e) 0,5 e 2,0
a) 165 ? m; 0,157 rad/min.
b) 165 ? m; 40 rad/min.
c) 160 ? m; 0,157 rad/min.
d) 150 ? m; 0,157 rad/min.
e) 150 ? m; 40 rad/min.
31) Levando-se em conta os conceitos de período T e freqüência f, marque a única opção correta:
a) O período de rotação da Terra em torno do Sol é menor que o da Lua em torno da Terra.
b) A freqüência de rotação do ponteiro dos minutos de um relógio é menor que a do ponteiro das horas.
c) A freqüência de rotação da Terra em torno do seu próprio eixo é maior que a de rotação da Lua em torno da Terra.
d) O período do ponteiro dos segundos de um relógio é maior que o do ponteiro das horas.
32) (AMAN) Um ponto material parte do repouso e se desloca sobre um plano horizontal em trajetória circular de 5,0 metros de raio com aceleração angular constante. Em 10 segundos o ponto material percorreu 100 metros. A velocidade angular do ponto material neste instante vale:
a) 16 rad . s-1
b) 4,0 rad . s-1
c) 20 rad . s-1
d) 2,0 rad . s-1
e) 0,40 rad . s-1
Soluções:
1)
? = ?o + y.t
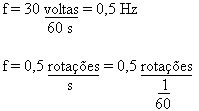
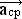 = w²R
= w²R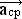 = (0,6)² · 5 = 1,8 cm/s².
= (0,6)² · 5 = 1,8 cm/s².
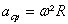
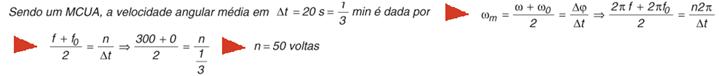
a) O período de rotação da Terra em torno do Sol é menor que o da Lua em torno da Terra.
b) A freqüência de rotação do ponteiro dos minutos de um relógio é menor que a do ponteiro das horas.
c) A freqüência de rotação da Terra em torno do seu próprio eixo é maior que a de rotação da Lua em torno da Terra.
d) O período do ponteiro dos segundos de um relógio é maior que o do ponteiro das horas.
32) (AMAN) Um ponto material parte do repouso e se desloca sobre um plano horizontal em trajetória circular de 5,0 metros de raio com aceleração angular constante. Em 10 segundos o ponto material percorreu 100 metros. A velocidade angular do ponto material neste instante vale:
a) 16 rad . s-1
b) 4,0 rad . s-1
c) 20 rad . s-1
d) 2,0 rad . s-1
e) 0,40 rad . s-1
33) (FUND. CARLOS CHAGAS) Uma roda gira em torno de seu eixo, de modo que um ponto de sua periferia executa um movimento circular uniforme. Excetuando o centro da roda, é correto afirmar que:
a) todos os pontos da roda têm a mesma velocidade escalar;
b) todos os pontos da roda têm aceleração centrípeta de mesmo módulo;
c) o período do movimento é proporcional à freqüência;
d) todos os pontos da roda têm a mesma velocidade angular;
e) o módulo da aceleração angular é proporcional à distância do ponto ao centro da roda.
34) (UCPR) Num local onde a aceleração da gravidade vale 10 m/s² uma pedra é abandonada de um helicóptero no instante em que este está a uma altura de 1000 m em relação ao solo. Sendo 20s o tempo que a pedra gasta para chegar ao solo, pode-se concluir que no instante do abandono da pedra o helicóptero: (Desprezam-se as resistências passivas)
a) subia
b) descia
c) estava parado
d) encontrava-se em situação indeterminada face aos dados;
e) esta situação é impossível fisicamente.
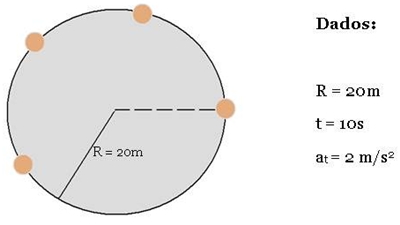
35) Um objeto inicia o seu movimento, a partir do repouso, deslocando-se numa trajetória circular de raio igual a 20 m. A sua aceleração tangencial tem módulo de 2 m/s2.
O objeto movimenta-se no sentido anti-horário. Após, 10 segundos.
Determine:
a) módulo da velocidade tangencial.
b) a aceleração angular.
c) a velocidade angular.
d) o comprimento do arco que o objecto percorreu durante os 10 s.
e) ângulo ? percorrido.
f) a aceleração centrípeta.
g) a aceleração total e qual é a sua direção.

1)
? = ?o + y.t
20. ? = 30. ? + y.2
2.y = -10. ?
y = -5. ? rad/s
2.y = -10. ?
y = -5. ? rad/s
a = y.r
a = -5.0,5
a = 2,5m/s²
2)
? = ?o + y.t
2.?.f = 2.?.fo + y.t
2.?.500 = 2.?.2000 + y.1,5
1000. ? = 4000.? + 1,5y
1,5y = -3000.?
y = -3000.?/1,5
y = -2000.? rad/s²
2.?.500 = 2.?.2000 + y.1,5
1000. ? = 4000.? + 1,5y
1,5y = -3000.?
y = -3000.?/1,5
y = -2000.? rad/s²
Como a = y.r
Temos que: a = -2000.?.2.10-3 = 4.?m/s²
3)
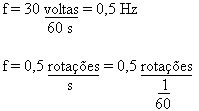
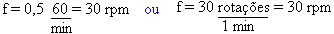
4)
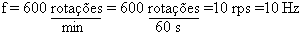
como 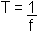

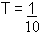
 T = 0,15
T = 0,15
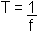

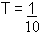
 T = 0,15
T = 0,155)
a) do enunciado o período é: T = 10 s
a freqüência 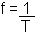

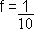 = 0,1 Hz
= 0,1 Hz
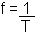

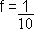 = 0,1 Hz
= 0,1 Hzb) a velocidade angular w
w = 2 pf = 2·p·0,1 = 0,2 p rad/s
w = 0,2·3 = 0,6 rad/s
w = 0,2·3 = 0,6 rad/s
c) a velocidade escalar
v = w R  v = 0,6· 5 = 3,0 cm/s
v = 0,6· 5 = 3,0 cm/s
 v = 0,6· 5 = 3,0 cm/s
v = 0,6· 5 = 3,0 cm/sd) o módulo da aceleração centrípeta
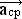 = w²R
= w²R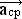 = (0,6)² · 5 = 1,8 cm/s².
= (0,6)² · 5 = 1,8 cm/s².6)
0,25 = ?² . 1
?² = 0,25
? = 0,5 rad/s
- Calculando T
? = 2?/T
0,5 = 2?/T
T = 2?/0,5
T = 4? s
Letra B.
7) Calculando a frequência, em hertz, temos:
f = 150/60
f = 2,5 hz
- Podemos agora calcular a velocidade linear:
v = 2?Rf
v =2? . 30 . 2,5
v = 150? cm/s
- Calculando a distância, temos:
d = v . ?t
d = 150? . 10
d = 1500? cm
Letra D.
8) D
9)
a) As velocidades angulares serão iguais, pois só dependem do período de rotação da terra, o mesmo para os dois.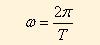
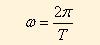
b) As frequências também serão iguais pelo mesmo motivo.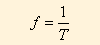
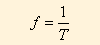
c) Os módulos das velocidades lineares serão diferentes, pois os raios são diferentes:
a velocidade linear é dada por: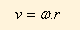
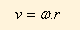
Para a pessoa que está na linha do equador a velocidade linear será maior, pois o raio é maior. Para a pessoa que está no trópico de Capricórnio o inverso.
d) a aceleração centrípeta é dada por:
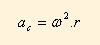
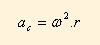
Logo, terão acelerações diferentes, pois os raios são diferentes.
Para a pessoa que está na linha do equador a aceleração centrípeta será maior, pois o raio é maior. Para a pessoa que está no trópico de Capricórnio o inverso.
10) T=6s --- f=1/3Hz
11)
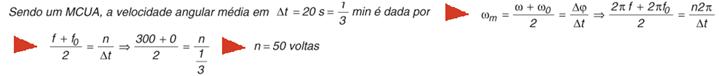
Letra D
12)
T = 2,0/1
T = 2,0 s
- Calculando a freqüência temos:
f = 1/T
f = 1/2,0
f = 0,50 Hz
- Como o corpo percorre uma volta (2p rad) em 2,0 segundos, podemos calcular a velocidade angular:
w = ?j/?t
w = 2p/2,0
w = p rad/s
28)
A frequência é a razão entre o número de voltas e o intervalo de tempo. Logo:
n°v = 1
t = 20 s
Logo:
f = 1/20
f = 0,05 Hz
Encontramos em Hz pois dividimos por um tempo em segundos. Para converter para rpm, multiplique por 60:
0,05 . 60 = 3 rpm
Letra C
33) D
34) A
35) a) Vt = a x t
 ? rad 180º
? rad 180º x 5,7º
x 5,7º
12)
Quando B partiu, A já havia efetuado, em t=4s, com WA= 1,5 rad/s --- ?=W.t=1,5.4 --- ?=6 rad --- fazendo os dois partirem juntos com ?oA=6rad e ?oB=0 --- equação de A --- ?A= ?oA + WA.t --- ?A= 6 + 1,5.t --- equação de B --- ?B= ?oB + WB.t ---
?B= 0 + 3.t --- quando se encontram pela primeira vez, B está uma volta completa (2?rad) na frente de A --- ?B ? ?A=2? ---
3t ? 6 ? 1,5t=2? --- 1,5t=2? + 6 --- t=12/1,5 --- t=8s
13)
Parando o corredor B, o A estará se afastando dele com velocidade relativa de VR=8 ? 6=2m/s e para ficar com uma volta de vantagem sobre ele deverá a distância correspondente a uma volta completa d=2?R=2.3.12,0=72,0m --- VR=d/t --- 2=72,0/t --- t=36, 0s --- ou, na forma angular --- ?A=VA/R=8/12,0=1/1,5 rad/s --- ?B=VB/R=6/12,0=1/2 rad/s --- velocidade angular relativa --- WR=WA ? WB=1/1,5 ? 1/2 --- WR=1/6 rad/s --- WR=??/?t --- 1/6=2?/t ---1/6=2.3/t --- t=36,0s --- ou ainda --- ?A= ?o + WA.t=0 + 1/1,5.t --- ?A= 1/1,5.t --- ?B= ?o + WB.t=0 + 1/2.t --- ?B= 1/2.t --- ?A - ?B=2? ---- 1/1,5t ? 1/2t = 2? --- t=36,0s
Letra E
14)
a) WA=2?/T=2?/6 --- WA= ?/3rad/s --- para retornar a P, A ?varreu? um ângulo de ??=2? rad --- WA=2?/t --- ?/3=2?t --- tA=6 s --- para retornar a P, B ?varreu? um ângulo de ??=2? rad --- WB=2?/t --- ?/6=2?t --- tA=12 s --- assim, eles se encontram em 12 s, quando B deu uma volta e A, duas; em 24 s quando o móvel B deu duas voltas e o móvel A quatro, e assim por diante.
b) Como eles se movem em sentidos contrários a velocidade relativa é a soma das velocidades --- WR=WA + WB=?/3 + ?/6 ---
WR=?/2 rad/s --- um deles pára e o outro se desloca com WR=?/2 rad/s e percorre até o encontro ??=2? rad --- WR=2?/t --- ?/2=2?/t t=4s --- se encontram de 4 s em 4s.
15)
Mesmo sentido (t=30s) --- ?B ? ?A=2? --- (2?/TB)t ? (2?/TA)t=2? --- 1/TB ? 1/TA=1/30 (I) --- sentidos opostos (t=10s) --- ?B + ?A=2? --- (2?/TB)t + (2?/TA)t=2? --- 1/TB + 1/TA=1/10 (II) --- resolvendo (I) com (II) --- TA=15s e TB=30s
16) f=1/1h=1/3.600 Hz --- T= 3.600 s --- Letra A.
17)
Comparando ? = ?/4 + ?/2.t com ? = ?o + W.t
a) ?o=?/4 rad
b) W=?/2 rad/s
c) t=8s --- ? = ?/4 + ?/2.t --- ? = ?/4 + ?/2.8 --- ? = ?/4 + 4? --- ? = 17?/4 rad --- como a cada volta ele efetua 2? rad ---
n=(17?/4)/2? --- n=8,5 voltas
d) Multiplicando cada membro da expressão ? = ?/4 + ?/2.t pelo raio R=4m --- ?.4 = (?/4).4 + (?/2).4.t --- S= ? + 2?t
18)

at=a=1m/s2 --- V=Vo ? at=0 ? 1.2 --- V=-2m/s2 --- ac=V2/R=4/1 --- ac=4m/s2 --- ?2=12 + 42 --- ?=?17 m/s2
19) A luz estroboscópica tem freqüência de 5Hz, ou seja, ilumina o pneu a cada T=1/f=1/5=0,2s --- assim, se a roda girasse ele com freqüência de 5Hz, ele veria a mancha branca sempre na mesma posição (a mancha daria uma volta completa a cada 0,2s) --- mas como ele vê a mancha como se o carro se movesse para trás, a mancha deve demorar menos que 0,2s para dar uma volta completa, assim --- T < 0,2s --- 1/f < 0,2 1/f <1/5 --- f < 5Hz --- Letra B.
20)
- Calculando o período temos:
T = ?t/nT = 2,0/1
T = 2,0 s
- Calculando a freqüência temos:
f = 1/T
f = 1/2,0
f = 0,50 Hz
- Como o corpo percorre uma volta (2p rad) em 2,0 segundos, podemos calcular a velocidade angular:
w = ?j/?t
w = 2p/2,0
w = p rad/s
21) Ao mesmo tempo em que a Lua translada em torno da Terra, ela também sofre a rotação em torno de seu eixo, mantendo sempre a mesma face para a Terra. Letra C
22) - O ponteiro das horas tem um período de 12 h e o ponteiro dos minutos tem um período de 1 h, portanto,o período do primeiro é maior que o segundo. Letra D.
23) a)
a.1) Dados Fórmula Resolução
T=? T=1/f T=1/2,5
f=2,5Hz T=0,40s
R: O período do movimento da partícula é de 0,40s
a.2) Dados Fórmula Resolução
v=? v=2?Rf v=2.3,14.0,20.2,5
R=0,20m v=6,28.0,5
f=2,5Hz v=3,14m/s
?=3,14
R: A velocidade linear da partícula é de 3,14m/s.
a.3) Dados Fórmula Resolução
?=? ?=2?f ?=2?.2,5
f=2,5Hz ?=5?
?=3,14 ?=5?rad/s
R: Como a partícula descreve atrajectória em sentido horário, o vector velocidade angular tem o sentido descendente e consequentemente de valor negativo. Então, o valor da velocidade angular do movimento da partícula é igual a -5?rad/s.
a.4) Dados Fórmula Resolução
ac=? ac=?2R ac=(-5?)2.0,20
?=-5?rad/s ac=(-15,7)2.0,20
R=0,20m ac=246,49.0,20
ac=49,298m/s2
R: A aceleração centrípeta do movimento da partícula é igual a 49,298m/s2
24) a) R: A expressão que relaciona a posição angular de uma partícula animada de m.c.u.v. com o tempo é:
?=?o+?ot+1/2?t2 Comparando esta expressão geral com
?=4-2t+2t2, temos:
a.1) R: ?o = 4rad
a.2) R: ?o = -2rad/s
a.3) 1/2? = 2 Û R: ? = 4rad/s2
25) D
26) Como ? = 2 .? . f , e f = 1/T , podemos dizer também que:
? = 2 . ? / T
Um ano tem 365 dias, que possuem 24 horas, cada hora com 60 minutos, e cada 60 minutos com 3600 segundos.
Logo, em um ano, possuimos:
60 . 60 . 24 . 365 = 31536000 segundos.
Aplicando:
? = 2 . ? / 31536000
Como a velocidade linear é:
V = ? . r
O raio é 150000000:
? = 2 . ? . 150000000 / 31536000
? = 30 km/s
Achamos em km/s pois multiplicamos rad/s por km.
Agora, sabemos que 30 km/s = 30000 m/s.
A aceleração centrípeta é calculada por:
Actp = v²/r
Agora teremos que usar o raio em metros e a velocidade em m/s. Para converter km para m, multiplique por 1000.
150.000.000 x 1000 = 150.000.000.000 m
Aplicando:
Actp = 30000²/150.000.000.000
Actp = 900.000.000/150.000.000.000
Actp = 0,006 m/s²
Letra C
26) Como ? = 2 .? . f , e f = 1/T , podemos dizer também que:
? = 2 . ? / T
Um ano tem 365 dias, que possuem 24 horas, cada hora com 60 minutos, e cada 60 minutos com 3600 segundos.
Logo, em um ano, possuimos:
60 . 60 . 24 . 365 = 31536000 segundos.
Aplicando:
? = 2 . ? / 31536000
Como a velocidade linear é:
V = ? . r
O raio é 150000000:
? = 2 . ? . 150000000 / 31536000
? = 30 km/s
Achamos em km/s pois multiplicamos rad/s por km.
Agora, sabemos que 30 km/s = 30000 m/s.
A aceleração centrípeta é calculada por:
Actp = v²/r
Agora teremos que usar o raio em metros e a velocidade em m/s. Para converter km para m, multiplique por 1000.
150.000.000 x 1000 = 150.000.000.000 m
Aplicando:
Actp = 30000²/150.000.000.000
Actp = 900.000.000/150.000.000.000
Actp = 0,006 m/s²
Letra C
28)
A frequência é a razão entre o número de voltas e o intervalo de tempo. Logo:
n°v = 1
t = 20 s
Logo:
f = 1/20
f = 0,05 Hz
Encontramos em Hz pois dividimos por um tempo em segundos. Para converter para rpm, multiplique por 60:
0,05 . 60 = 3 rpm
Letra C
29) A frequência é calculada pela razão entre o número de voltas e o tempo. Logo,
f = n° v/t
Dados:
n° v = 0,5
t = 2 s
f = ?
Aplicando:
f = 0,5/2
f = 0,25 Hz
A frequência de movimento é de 0,25 Hz
Já o período é calculado pela razão entre o tempo e a quantidade de voltas, ou seja, o inverso do período:
p = 1 / f
Logo,
T = 1 / 0,25
T = 4 s
O período de rotação é de 4 segundos.
Alternativa C
30) D
31) a) A Terra demora 365 dias para dar uma volta em torno do Sol e a Lua cerca de 28 dias para dar uma volta na Terra. Logo, o período da Terra é maior.
b) f = 1/T . O ponteiro dos minutos dá a volta mais rápida, logo, tem menor período e maior freqüência que o das horas.
c) A Terra demora 1 dia para dar a volta em seu eixo e a Lua, como dissemos, cerca de 28 para voltear a Terra. Logo, a Terra tem período menor e freqüência maior, já que esta é o inverso do período.
d) O ponteiro dos segundos demora 1 minuto para dar uma volta e o das horas 12 h.
f = n° v/t
Dados:
n° v = 0,5
t = 2 s
f = ?
Aplicando:
f = 0,5/2
f = 0,25 Hz
A frequência de movimento é de 0,25 Hz
Já o período é calculado pela razão entre o tempo e a quantidade de voltas, ou seja, o inverso do período:
p = 1 / f
Logo,
T = 1 / 0,25
T = 4 s
O período de rotação é de 4 segundos.
Alternativa C
30) D
31) a) A Terra demora 365 dias para dar uma volta em torno do Sol e a Lua cerca de 28 dias para dar uma volta na Terra. Logo, o período da Terra é maior.
b) f = 1/T . O ponteiro dos minutos dá a volta mais rápida, logo, tem menor período e maior freqüência que o das horas.
c) A Terra demora 1 dia para dar a volta em seu eixo e a Lua, como dissemos, cerca de 28 para voltear a Terra. Logo, a Terra tem período menor e freqüência maior, já que esta é o inverso do período.
d) O ponteiro dos segundos demora 1 minuto para dar uma volta e o das horas 12 h.
Assim, o período do ponteiro dos segundos é menor que o das horas. OPÇÃO: C.
32) B33) D
34) A
35) a) Vt = a x t
Û Vt = 2 x 10 = 20 m/s
b) at = constante = 2 m/s2
at = ? x R
Û ? = at/R
Û ? = 2/20 = 0,1 rad/s2
c) ? (t) = ?o + ?.t
Û ? (t) = 0 + 0,1 + 10
Û ? (t) = 1 rad/s
d) s (t) = so + vto.t + 1/2 .at.t2
Û s (t) = 0 + 0 + 1/2 .at.t2
Û s (t) = 1/2 x 2 x 102
Û s (t) = 100m
e) ? (t) = ?o + ?o.t + 1/2 .?.t2
Û ? (t) = 0 + 0 + 1/2 .?.t2
Û ? (t) = 1/2 x 0,1 x 102
Û ? (t) = 5 rad ou 286,5º
Cálculos Auxiliares
? rad 180º
5 rad x
x = 286.5º
f) ac = v2/20
Û ac = 202/20
Û ac = 20 m/s2
g) atotal = 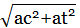
Û atotal =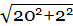
Û atotal = 20,1 m/s2
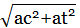
Û atotal =
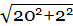
Û atotal = 20,1 m/s2
tg (?) = at/ac
Û tg (?) = 2/20
Û tg (?) = 0,1
tg-1 (0,1) ? 5,7º
ou
 ? rad 180º
? rad 180º x = 0,10 rad
 x 5,7º
x 5,7º Assim, em t = 10 s, o objeto:
a) Terá uma velocidade de 20 m/s.
b) A sua aceleração angular é de 0,1 rad/s2.
c) Terá uma velocidade angular de 1 rad/s.
d) Terá percorrido uma distância de s = 100m.
e) Estará na posição ? = 5 rad ou 286,5º.
f) A sua aceleração tangencial é de 2 m/s2.
g) A aceleração total é de 20,1 m/s2 e faz um ângulo de 0,10 rad com a direcção radial, apontando para o centro da trajetória.
- Leis De Kepler - Resumo (com Questões)
Primeira Lei de Kepler (Lei das órbitas) Primeira Lei de Kepler é a lei das órbitas, que diz:?? Todos os planetas se movem em orbitas elípticas tendo o Sol como um dos focos?? (HALLIDAY, David, Física 2, pg. 14.)...
- Vetores - Resumo (com Questões)
Grandezas escalares e vetoriaisAlgumas grandezas físicas exigem, para sua perfeita caracterização, apenas uma intensidade. Essas grandezas são denominadas grandezas escalares. Assim, grandezas físicas, como massa, comprimento, tempo,...
- Movimento Uniforme (mu) E Movimento Uniformemente Variado (muv) - Resumo (com Questões)
Definição de movimento uniforme A tartaruga é um bicho estranho. Pode o mundo cair ao seu redor que ela continua se movimentando sem alterar a sua velocidade. Depois que ela sai do repouso e entra em movimento, ela dificilmente varia sua velocidade...
- Velocidade Escalar Média E Deslocamento Escalar: Exemplos E Questões Resolvidas
Artigo sobre velocidade escalar média, trajetória, intervalo de tempo e deslocamento com questões resolvidas. Velocidade escalar média A velocidade escalar média é a relação entre o deslocamento escalar ?s e o correspondente intervalo...
- área Do Setor Circular Questões
Área do setor circular Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo ??r², onde ? equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois...