Vestibular
O que estudaremos são grandezas que sejam diretamente ou inversamente proporcionais, embora existam casos em que essas relações não se observem, e que portanto, não farão parte de nosso estudo.
Por exemplo, "na partida de abertura de um campeonato, um jogador fez três gols, quantos gols ele fará ao final do campeonato sabendo que o mesmo terá 46 partidas?".
Grandezas Diretamente Proporcionais (G.D.P.)
Duas grandezas são ditas diretamente proporcionais, quando o aumento de uma implica no aumento da outra, quando a redução de uma implica na redução da outra, ou seja, o que você fizer com uma acontecerá com a outra.
Observação é necessário que satisfaça a propriedade destacada abaixo.
Exemplo: Se numa receita de pudim de microondas uso duas latas de leite condensado, 6 ovos e duas latas de leite, para um pudim. Terei que dobrar a quantidade de cada ingrediente se quiser fazer dois pudins, ou reduzir a metade cada quantidade de ingredientes se quiser, apenas meia receita.
Observe a tabela abaixo que relaciona o preço que tenho que pagar em relação à quantidade de pães que peça:
Preço e quantidade de pães são grandezas diretamente proporcionais. Portanto se peço mais pães, pago mais, se peço menos pães, pago menos. Observe que quando dividimos o preço pela quantidade de pães obtemos sempre o mesmo valor.
Propriedade: Em grandezas diretamente proporcionais, a razão é constante.

Grandezas Inversamente Proporcionais (G.I.P.)
Duas grandezas são ditas inversamente proporcionais quando o aumento de uma implica na redução da outra, quando a redução de uma implica no aumento da outra, ou seja, o que você fizer com uma acontecerá o inverso com a outra.
Observação: É necessário que satisfaça a propriedade destacada abaixo.
Exemplo: Numa viagem, quanto maior a velocidade média no percurso, menor será o tempo de viagem. Quanto menor for a velocidade média, maior será o tempo de viagem.
Observe a tabela abaixo que relaciona a velocidade média e o tempo de viagem, para uma distância de 600km.
Velocidade média e Tempo de viagem são grandezas inversamente proporcionais, assim se viajo mais depressa levo um tempo menor, se viajo com menor velocidade média levo um tempo maior. Observe que quando multiplicamos a velocidade média pelo tempo de viagem obtemos sempre o mesmo valor.
Propriedade: Em grandezas inversamente proporcionais, o produto é constante.
50 x 10 = 500 = 4 x 150 = 5 x 100 = K
Exercícios resolvidos sobre grandezas proporcionais
1) Os números x, y e 32 são diretamente proporcionais aos números 40, 72, 128. Determine os números x e y.
3) Três funcionários arquivaram um total de 382 documentos em quantidades inversamente proporcionais às suas respectivas idades: 28, 32 e 36 anos. Nessas condições, é correto afirmar que
O Z irá representar o funcionário com 36 anos.
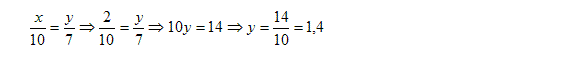
Se x, y e z são inversamente proporcionais a 10, 1 e 5, então podemos dizer que x, y e z são diretamente proporcionais aos seus inversos multiplicativos, ou seja:
Temos então:
Substituindo os valores acima na expressão dada y - z2 - 2x = 0, vem:
Dividindo ambos os membros por 4, vem:
Como o enunciado do problema diz que x é positivo, vem que somente o valor x = 2 serve. Ora, se x = 2, então

11) Um garoto de 1m de altura projeta uma sombra de 0,5 m. No mesmo instante, um edifício projeta uma sombra de 9 m. Qual é altura do edifício?
Solução:
Seja H a altura do edifício. A altura e a sombra são grandezas diretamente proporcionais. Então, temos a proporção: 1 / 0,5 = H / 9. O que implica em H = 9 / 0,5 = 90 / 5 = 18 m
Por outro lado, como a sombra e a altura formam um ângulo de 90 graus, segue que a sombra e a altura são catetos de um triãngulo retângulo. Logo, temos dois triângulos retângulos semelhantes.
Pelo Teorema de Tales, os lados correspondentes dos triângulos semelhantes são proporcionais.
Então, temos a proporção:
1 / 0,5 = H / 9. Assim, H = 9 / 0,5 = 90 / 5 = 18 m .
NOTA: Em trigonometria dizemos a razão H/S = h/s é a tangente do ângulo a (tg a).
12) (Ag. de Trânsito - Cesgranrio - 2005) Uma equipe de 30 agentes de trânsito vai ser dividida em dois grupos que atuarão em duas regiões diferentes, uma de 6 km² e outra, de 9 km². Se essa equipe for dividida em partes diretamente proporcionais às áreas das duas regiões, quantos agentes trabalharão na região de maior área?
(A) 18 (B) 15 (C) 12 (D) 9 (E) 6
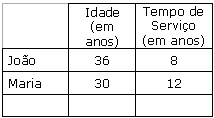
13) (Prova Técnico Judiciário ? Área Administrativa ? 4ª Região) - No quadro abaixo, têm-se as idades e os tempos de dois técnicos judiciários do Tribunal Regional Eleitoral de uma certa circunscrição judiciária.
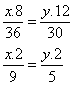
- Cubo E Paralelepípedo Questões Vestibular
Questões de vestibular sobre cubo e paralelepípedo 1) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4? d² = 2² + 2² d² = 8 d = 2?22) Se um cubo tem suas arestas aumentadas em...
- Semelhança De Figuras Planas
Artigo sobre semelhança de figuras planas. Para que duas ou mais figuras (ou objetos) sejam semelhantes, três condições são necessárias: Os ângulos correspondentes devem ser iguais. Os comprimentos correspondentes devem ser proporcionais. Possuir...
- Regra De Três Simples E Composta Método Prático
Artigo com método prático para a solução de regra de três simples e composta. Um automóvel percorre um espaço de 480 Km em 02 horas. Quantos kms ele percorrerá em 06 horas? Grandeza 1: Distância percorridaGrandeza 2: Tempo necessário Cálculo:Distância...
- Questões Regra De Três Composta
1) (FUB-94 / Auxiliar Administrativo) Em uma loja, o metro de um determinado tecido teve seu preço reduzido de R$ 5,52 para R$ 4.60. Com R$ 126,96, a porcentagem de tecido que se pode comprar a mais é de :a) 19,5 % b) 20% ...
- Razão Exemplos E Exercícios
Artigo sobre razão com exemplos e exercícios resolvidos É a forma de se comparar duas grandezas, mas é necessário para isto que as duas estejam na mesma unidade de medida. Indica-se a razão de a para b por a / b...
Vestibular
grandezas diretamente e inversamente proporcionais exercícios resolvidos
O que estudaremos são grandezas que sejam diretamente ou inversamente proporcionais, embora existam casos em que essas relações não se observem, e que portanto, não farão parte de nosso estudo.
Por exemplo, "na partida de abertura de um campeonato, um jogador fez três gols, quantos gols ele fará ao final do campeonato sabendo que o mesmo terá 46 partidas?".
Grandezas Diretamente Proporcionais (G.D.P.)
Duas grandezas são ditas diretamente proporcionais, quando o aumento de uma implica no aumento da outra, quando a redução de uma implica na redução da outra, ou seja, o que você fizer com uma acontecerá com a outra.
Observação é necessário que satisfaça a propriedade destacada abaixo.
Exemplo: Se numa receita de pudim de microondas uso duas latas de leite condensado, 6 ovos e duas latas de leite, para um pudim. Terei que dobrar a quantidade de cada ingrediente se quiser fazer dois pudins, ou reduzir a metade cada quantidade de ingredientes se quiser, apenas meia receita.
Observe a tabela abaixo que relaciona o preço que tenho que pagar em relação à quantidade de pães que peça:
| Preço R$ | 0,20 | 0,40 | 1,00 | 2,00 | 4,00 | 10,00 |
| Nº de pães | 1 | 2 | 5 | 10 | 20 | 50 |
Preço e quantidade de pães são grandezas diretamente proporcionais. Portanto se peço mais pães, pago mais, se peço menos pães, pago menos. Observe que quando dividimos o preço pela quantidade de pães obtemos sempre o mesmo valor.
Propriedade: Em grandezas diretamente proporcionais, a razão é constante.

Grandezas Inversamente Proporcionais (G.I.P.)
Duas grandezas são ditas inversamente proporcionais quando o aumento de uma implica na redução da outra, quando a redução de uma implica no aumento da outra, ou seja, o que você fizer com uma acontecerá o inverso com a outra.
Observação: É necessário que satisfaça a propriedade destacada abaixo.
Exemplo: Numa viagem, quanto maior a velocidade média no percurso, menor será o tempo de viagem. Quanto menor for a velocidade média, maior será o tempo de viagem.
Observe a tabela abaixo que relaciona a velocidade média e o tempo de viagem, para uma distância de 600km.
| Velocidade média (km/h) | 60 | 100 | 120 | 150 | 200 | 300 |
| Tempo de viagem (h) | 10 | 6 | 5 | 4 | 3 | 2 |
Velocidade média e Tempo de viagem são grandezas inversamente proporcionais, assim se viajo mais depressa levo um tempo menor, se viajo com menor velocidade média levo um tempo maior. Observe que quando multiplicamos a velocidade média pelo tempo de viagem obtemos sempre o mesmo valor.
Propriedade: Em grandezas inversamente proporcionais, o produto é constante.
50 x 10 = 500 = 4 x 150 = 5 x 100 = K
Exercícios resolvidos sobre grandezas proporcionais
1) Os números x, y e 32 são diretamente proporcionais aos números 40, 72, 128. Determine os números x e y.
Solução:
128/32 = 4
Então,
x = 40 / 4 = 10
y = 72 / 4 = 18
2) Sabendo que x, y, z e 120 são diretamente proporcionais aos números 150, 120, 200 e 600, determine os números a, b e c.
Solução:
600/120 = 5
Então,
x = 150/5 = 30
y= 120/5 = 24
z = 200/5 = 40
3) Três funcionários arquivaram um total de 382 documentos em quantidades inversamente proporcionais às suas respectivas idades: 28, 32 e 36 anos. Nessas condições, é correto afirmar que o número de documentos arquivados pelo funcionário mais velho foi:
Solução:
Agora vamos separar algumas informações:
O X irá representar o funcionário com 28 anos.
O Y irá representar o funcionário com 32 anos.
O Z irá representar o funcionário com 36 anos.
K = x + y + z
1/28 + 1/32 + 1/36
Veja que: X + Y + Z é igual a 382. Então:
K = 382
1/28 + 1/32 + 1/36
O MMC de 28, 32 e 36 é 2016. Sendo assim:
K = 382
72/2016 + 63/2016 + 56/2016
K = 382
191/2016
K = 382 * 2016
191
K = 4032
Nós queremos saber somente quantos documentos foram arquivados pelo funcionário mais velho. Dessa forma:
1/36 * 4032 = 112
A resposta é:
O funcionário mais velho arquivou 112 documentos.
4) Na bandeira brasileira, o comprimento e a largura são proporcionais a 10 e 7. Carla quer fazer uma bandeira com 2 m de comprimento. Quantos metros deverá ter a largura?
a) 1,20 b) 1,30 c) 1,40 d) 1,50 e) 1,70
Se a bandeira apresenta 2 metros de comprimento, sendo as medidas proporcionais a 10 e 7, temos que estabelecer uma proporção, ou seja:
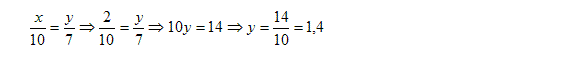
5) Os números positivos x, y e z são inversamente proporcionais a 10, 1 e 5.
Sabendo-se que y - z2 - 2x = 0, determine x + y + z .
Se x, y e z são inversamente proporcionais a 10, 1 e 5, então podemos dizer que x, y e z são diretamente proporcionais aos seus inversos multiplicativos, ou seja:
x, y e z são diretamente proporcionais a 1/10, 1/1 e 1/5.
Assim, poderemos escrever a seguinte relação de proporcionalidade direta:
x / (1/10) = y / (1/1) = z / (1/5)
Daí, vem, após efetuarmos as divisões indicadas:
10x = y = 5z
Temos então:
10x = 5z, de onde tiramos: z = 2x (dividindo ambos os membros por 5).
10x = y, de onde tiramos: y = 10x
Substituindo os valores acima na expressão dada y - z2 - 2x = 0, vem:
10x - (2x)2 - 2x = 0
10x - 4x2 - 2x = 0
8x - 4x2 = 0
Dividindo ambos os membros por 4, vem:
2x - x2 = 0
Colocando x em evidencia, vem: x(2 - x) = 0 e, portanto, x = 0 ou x = 2.
Como o enunciado do problema diz que x é positivo, vem que somente o valor x = 2 serve. Ora, se x = 2, então
y = 10x = 10(2) = 20 e z = 2x = 2(2) = 4.
Assim, a soma x + y + z = 2 + 20 + 4 = 26.
6) Se João correr a uma velocidade de 4,0 km/h, ele completa uma certa distância em 6 minutos. Em 8 minutos, com a mesma distância, sua velocidade será:
a) 5,3 km/h b) 5,2 km/h c) 7,6 km/h d) 3,0 km/h
O primeiro passo é identificar a proporcionalidade inversa entre as grandezas, velocidade e tempo. É fácil perceber que quanto mais veloz é um móvel menor é o tempo gasto para percorrer uma determinada distância. Quanto maior a velocidade menor é o tempo, essa característica garante a proporcionalidade inversa.
O segundo passo é montar a regra de três e calcular a velocidade de João se ele percorrer a distância proposta em 8 minutos, tem-se:
Se João percorrer a mesma distância em 8 minutos sua velocidade será 3,0 km/h. Alternativa D.
7) Determine quantos quilômetros esse automóvel percorre, em média, com 1 litro desse combustível.
Solução:
A razão de duas ou mais grandezas de mesma espécie é o quociente dos números que expressam as suas medidas, consideradas na mesma unidade. O conceito de razão nos permite fazer comparações de grandeza entre dois números. Indica explicitamente quantas vezes o primeiro número contém o segundo (não necessariamente um valor inteiro). Toda fração é também uma razão, mas nem toda razão pode ser expressa como uma fração. A fração é uma forma de expressar o quociente de dois números inteiros enquanto que a razão é o resultado do quociente entre dois números. A igualdade entre razões denomina-se proporção.
Se o quilômetro percorrido aumenta, o consumo médio de combustível (em litros) também aumenta na mesma proporção (grandezas diretamente proporcionais). Dizemos que 12,5 litros está para 100 km assim como 1 litro está para x km.
Seja a proporção: 12,5 /100 = 1/x , onde x é o valor procurado.
Multiplicando "em cruz", segue que: 12,5x = 100
x = 100/12,5 = 1000/125 = 8
Logo, com 1 litro, esse automóvel percorre em em média 8 km.
8) Na bula de um determinado remédio pediátrico recomenda-se a seguinte dosagem: 5 gotas para cada 2 kg do "peso" da criança. Se uma criança tem 12 kg, qual a dosagem correta?
Solução:
Se o peso da criança aumenta, a dosagem também aumenta na mesma proporção (grandezas diretamente proporcionais), ou seja, 5 gotas está para 2 kg assim como x gotas está para 12 kg. Portanto, temos a proporção: 5/2 = x/12.
Multiplicando "em cruz", segue que 2x = 60.
Logo x = 60/2 = 30 gotas.
9) (TRE) Para executar a tarefa de manutenção de 111 microcomputadores, três técnicos judiciários dividiram o total de microcomputadores entre si, na razão inversa de suas respectivas idades: 24, 30 e 36 anos. Assim sendo, quanto recebeu o técnico de 30 anos?
Resolução:
Sendo A a parte do mais novo, B a parte que cabe ao do meio, C a parte do mais velho, vamos usar um método conhecido como: DIVISÃO EM PARTES INVERSAMENTE PROPORCIONAIS. Desse modo, temos a proporção:
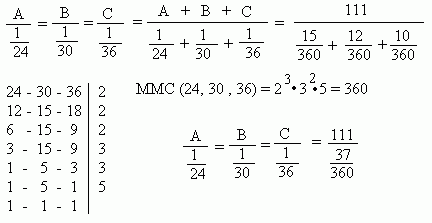
Logo: 24A = 30B = 36C = 1080
A = 1080/24 = 45;
B = 1080/30 = 36;
C = 1080/36 = 30 .
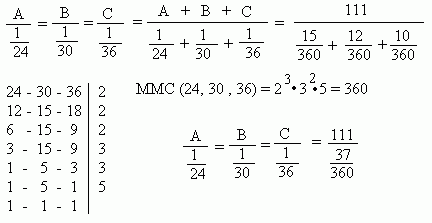
Logo: 24A = 30B = 36C = 1080
A = 1080/24 = 45;
B = 1080/30 = 36;
C = 1080/36 = 30 .
Assim, o técnico de 30 anos recebeu 36 computadores.
10) (ENEM) A sombra de uma pessoa que tem 1,80 m de altura mede 60 cm. No mesmo momento, a seu lado, a sombra projetada de um poste mede 2,00 m. Se, mais tarde, a sombra do poste diminuiu 50cm, a sombra da pessoa passou a medir quanto?
Solução:
Temos que 2,00 m = 200 cm e 1,80 m = 180 cm. Como a altura e a sombra são grandezas diretamente proporcionais, temos a proporção:
180/60 = H/200, onde H é a altura do poste.
Vem que, 3 = H/200 , o que implica em: H = 3 × 200 = 600 cm. Mais tarde teremos a proporção:
180/x = 600/(200-50) = 600/150 = 4.
Então, 180 = 4x. Logo: x = 180/4 = 45 cm.
Este problema poderia ser resolvido de outra maneira.
Observe que a sombra do poste diminuiu de 50/200 = 1/4.
Então a sombra da pessoa também diminuiu de 1/4.
Segue que a sombra da pessoa diminuiu de 1/4 × 60 = 15.
Logo, a sombra da pessoa passou a medir: 60 - 15 = 45 cm.
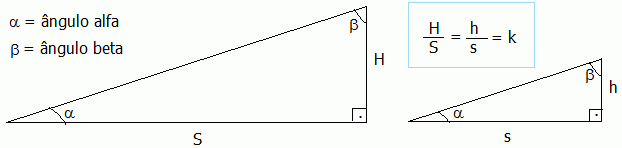
11) Um garoto de 1m de altura projeta uma sombra de 0,5 m. No mesmo instante, um edifício projeta uma sombra de 9 m. Qual é altura do edifício?
Solução:
Seja H a altura do edifício. A altura e a sombra são grandezas diretamente proporcionais. Então, temos a proporção: 1 / 0,5 = H / 9. O que implica em H = 9 / 0,5 = 90 / 5 = 18 m
Por outro lado, como a sombra e a altura formam um ângulo de 90 graus, segue que a sombra e a altura são catetos de um triãngulo retângulo. Logo, temos dois triângulos retângulos semelhantes.

Pelo Teorema de Tales, os lados correspondentes dos triângulos semelhantes são proporcionais.
Então, temos a proporção:
1 / 0,5 = H / 9. Assim, H = 9 / 0,5 = 90 / 5 = 18 m .
NOTA: Em trigonometria dizemos a razão H/S = h/s é a tangente do ângulo a (tg a).
12) (Ag. de Trânsito - Cesgranrio - 2005) Uma equipe de 30 agentes de trânsito vai ser dividida em dois grupos que atuarão em duas regiões diferentes, uma de 6 km² e outra, de 9 km². Se essa equipe for dividida em partes diretamente proporcionais às áreas das duas regiões, quantos agentes trabalharão na região de maior área?
(A) 18 (B) 15 (C) 12 (D) 9 (E) 6
13) (Prova Técnico Judiciário ? Área Administrativa ? 4ª Região) - No quadro abaixo, têm-se as idades e os tempos de dois técnicos judiciários do Tribunal Regional Eleitoral de uma certa circunscrição judiciária.

Esses funcionários foram incumbidos de digitar as laudas de um processo. Dividiram o total de laudas entre si, na razão direta de suas idades e inversa de seus tempos de serviço no Tribunal. Se João digitou 27 laudas, o total de laudas do processo era:
a) 40
b) 41
c) 42
d) 43
e) 44
Solução:
Uma razão é uma divisão entre duas grandezas. Exemplo: a velocidade é uma razão determinada pela divisão entre a grandeza distância e a grandeza tempo.
Na questão proposta na prova, exige-se do candidato o conhecimento do que é uma divisão proporcional.
É preciso conhecer, portanto, o que são grandezas diretamente ou inversamente proporcionais.
Recapitulando:
Uma pessoa vai de SP a MG (percorrendo uma distância hipotética de 800 km) em 8h, fazendo a velocidade média de 100 km/h.
Se ao invés de ir para MG, resolvesse aumentar minha viagem para outra cidade mais distante, ou seja, crescendo a quilometragem percorrida para 1600 km, será que o tempo de viagem seria menor ou maior ? Considerando uma mesma velocidade?
De fato, levaria mais tempo, e ainda é possível afirmar que se a distância aumentou para o dobro (de 800 para 1600), o tempo também irá aumentar (de 8horas para 16 horas) e isto é possível verificar através das seguintes expressões:
D = V/T
(SP => MG) 800 = 100/T, logo T = 8 horas
(MG => Outra Cidade) 1600 = 100/T, logo T = 16 horas
É possível afirmar que distância e tempo são grandezas diretamente proporcionais.
Se diminuir a velocidade do carro pela metade será que eu vou levar mais ou menos tempo para viajar, considerando a mesma distância?
Se velocidade do carro diminuir, torna-se claro que vou levar menos horas para viajar, e portanto, quanto menos rápido for o carro mais tempo eu levo.
Desse modo é possível afirmar que a velocidade e o tempo são grandezas inversamente proporcionais.
Se duas grandezas são diretamente proporcionais, então quando uma aumenta a outra aumenta proporcionalmente e entre elas existe uma relação direta de proporcionalidade (m), desta forma:
A/B = m
Assim, se duas grandezas são inversamente proporcionais, então quando uma aumenta a outra diminui proporcionalmente e posso afirmar que entre elas existe uma relação inversa de proporcionalidade (m), desta forma:
A.B = m
No problema, as laudas devem ser divididas na relação direta das idades de João e Maria, e na relação inversa de seus tempos de serviço no Tribunal:
Logo:
Para x = 27
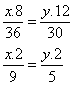
Substituindo x = 27
2y/5 = 6
y = 30/2 = 15
O número total de laudas é dado pela soma das laudas de João (x=27) com as de Maria (y=15) perfazendo o total de 42 laudas
Resposta: Letra ?c?
- Cubo E Paralelepípedo Questões Vestibular
Questões de vestibular sobre cubo e paralelepípedo 1) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4? d² = 2² + 2² d² = 8 d = 2?22) Se um cubo tem suas arestas aumentadas em...
- Semelhança De Figuras Planas
Artigo sobre semelhança de figuras planas. Para que duas ou mais figuras (ou objetos) sejam semelhantes, três condições são necessárias: Os ângulos correspondentes devem ser iguais. Os comprimentos correspondentes devem ser proporcionais. Possuir...
- Regra De Três Simples E Composta Método Prático
Artigo com método prático para a solução de regra de três simples e composta. Um automóvel percorre um espaço de 480 Km em 02 horas. Quantos kms ele percorrerá em 06 horas? Grandeza 1: Distância percorridaGrandeza 2: Tempo necessário Cálculo:Distância...
- Questões Regra De Três Composta
1) (FUB-94 / Auxiliar Administrativo) Em uma loja, o metro de um determinado tecido teve seu preço reduzido de R$ 5,52 para R$ 4.60. Com R$ 126,96, a porcentagem de tecido que se pode comprar a mais é de :a) 19,5 % b) 20% ...
- Razão Exemplos E Exercícios
Artigo sobre razão com exemplos e exercícios resolvidos É a forma de se comparar duas grandezas, mas é necessário para isto que as duas estejam na mesma unidade de medida. Indica-se a razão de a para b por a / b...
