Vestibular
Impulso e quantidade de movimento
Dizemos que uma força produz um impulso sobre um corpo quando ela age no corpo durante um certo intervalo de tempo.

No Sistema Internacional (SI), a unidade da grandeza impulso é N · s (newton vezes segundo). Como
N = kg · m/s2, temos:
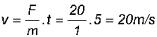
Se uma força tiver direção constante e intensidade variando no decorrer do tempo, seu impulso será calculado por meio da área sob o gráfico força × tempo.
Nesse caso, podemos definir uma força média como sendo a força constante capaz de produzir o mesmo impulso da força de intensidade variável. Isto é:

Como a quantidade de movimento é uma grandeza vetorial, apresenta módulo, direção e sentido, temos:
De acordo com o SI, a quantidade de movimento tem como unidade
kg · m/s (quilograma vezes metro por segundo).
Repare que a unidade de quantidade de movimento coincide com a de impulso, embora sejam grandezas diferentes.
Considere uma partícula de massa (m) constante, em movimento retilíneo uniformemente variado (MRUV).
De acordo com a 2a lei de Newton, a força resultante relaciona-se com a mudança de velocidade da partícula, num certo intervalo de tempo, assim:
Ou seja:


Embora tenhamos demonstrado o Teorema do Impulso a partir de uma situação simples de MRUV, sua aplicação é geral, estendendo-se a qualquer tipo de movimento, sob a ação de forças constantes ou variáveis.
A quantidade de movimento (ou momento linear) de um conjunto de partículas corresponde à soma vetorial das quantidades de movimento de cada partícula de tal sistema.
Considere, por exemplo, o conjunto formado por três partículas (A, B e C), abaixo indicadas, em que se destaca o vetor quantidade de movimento ( = m · ) que cada uma apresenta em um certo instante.
Obtemos o vetor quantidade de movimento do sistema
( sist), nesse instante, pela seguinte adição vetorial:
Se as velocidades das partículas tivessem a mesma direção, poderíamos obter o valor da quantidade de movimento do sistema através das velocidades escalares das partículas assim:
Em um sistema podem agir forças internas e externas. São chamadas de forças internas aquelas que são trocadas entre as partículas do sistema. Por constituírem pares ação-reação, o impulso total devido às forças internas sempre será nulo.
Uma força é classificada como externa quando é exercida no sistema pelo meio externo a ele. Essa força pode ser de ação a distância (força de campo) ou de contato.
Dizemos que um sistema de partículas é mecanicamente isolado quando for nulo o impulso total das forças externas sobre as partículas do sistema. Ou seja, o sistema será considerado isolado quando:
a) nenhuma força externa atuar, ou a resultante das forças externas for nula;
b) as forças externas forem desprezíveis, se comparadas com as forças internas;
c) a interação com o meio externo tiver uma duração muito pequena ( 0).
Todos os fatores acima nos permitem, portanto, eleger como sistemas isolados usuais os conjuntos de partículas associados aos fenômenos de colisão e explosão.
Por exemplo, observe abaixo a separação de massas (explosão) que uma mola inicialmente comprimida consegue produzir, quando interposta entre dois carrinhos (A e B) dispostos num plano horizontal liso.
Note que no conjunto (A + B + mola) as forças elásticas internas ( e ? ) são as que produzem a separação de A e B, enquanto as forças externas (pesos e normais) têm resultante nula. Logo, temos um sistema isolado.
Figura 1. Colisão de duas bolas de massas diferentes, com velocidades diferentes antes da colisão

Figura 1.1 - Carro e caminhão se movimentando em sentidos contrários, mesma direção e com velocidades iguais
Figura 1.2 - Dois blocos A e B ligados por uma mola
Figura 10.5 - Colisão de duas bolas de bilhar.Análise vetorial
Neste módulo, trataremos da mecânica relacionada às colisões frontais de partículas. A colisão entre dois corpos é denominada frontal ou unidimensional quando não ocorre mudança na direção da velocidade desses corpos, ou seja, as velocidades dos corpos, antes e depois do choque, possuem a mesma direção.
Sabemos que nas colisões há conservação da quantidade de movimento do sistema. Isto é: no choque entre duas partículas A e B, as quantidades de movimento de cada partícula variam, mas a quantidade de movimento do sistema se conserva.
Para um choque frontal, podemos escrever a equação de conservação de quantidade de movimento do sistema usando velocidades escalares, ou seja, atribuindo um sinal algébrico às velocidades das partículas de acordo com a orientação (positiva) definida para a trajetória.
Embora sempre ocorra a conservação da quantidade de movimento do sistema, numa colisão pode ou não haver conservação de energia mecânica do sistema.
Os choques são classificados em função da conservação ou não da energia cinética do sistema. Quando a energia cinética do sistema imediatamente após o choque é igual à energia cinética do sistema imediatamente antes do choque, ele recebe o nome de choque perfeitamente elástico. Se as energias cinéticas do sistema antes e após o choque forem diferentes, ele recebe o nome de choque não-elástico.
Tais denominações foram originadas em experiências com choques frontais entre um móvel e um anteparo rígido (uma parede, por exemplo).
Suponha que um carrinho se aproxime frontalmente de uma parede a 10 m/s e, após o choque, se afaste desta com velocidade de módulo 6 m/s.
Após o choque, o carrinho tem restituída apenas 60% da velocidade, em módulo, que possuía antes do choque. Conclusão: houve perda de energia cinética nessa colisão.
A partir disso, criou-se um coeficiente de restituição (e) para as colisões frontais, definido pela razão entre o módulo da velocidade de afastamento (após o choque) e o módulo da velocidade de aproximação (antes do choque).
Caso ocorresse 100% de restituição do módulo da velocidade (vafast. = vaprox.), o coeficiente de restituição atingiria seu valor máximo (e = 1) e não haveria perda de energia mecânica. Esse choque, denominado perfeitamente elástico, pode ser simulado lançando-se o carrinho contra uma mola ideal fixa numa parede, como mostra a figura abaixo.
Entre os choques não-elásticos, destaca-se o choque perfeitamente inelástico, no qual se produz a maior perda de energia mecânica. Este choque ocorre quando o coeficiente de restituição é mínimo, ou seja, igual a zero (e = 0). Num choque desse tipo, o carrinho lançado contra a parede não retornaria (grudar-se-ia nesta) e, por conseguinte, perderia toda sua energia mecânica inicial.
Sintetizando, podemos comparar os tipos de choques frontais assim:

Dessa forma, o coeficiente de restituição será obtido pela razão entre as velocidades relativas, depois e antes do choque, assim:
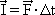
 I = 90 N.s
I = 90 N.s

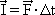
 F =
F =  = 5 N
= 5 N
3) Determine durante quanto tempo deve agir uma força de intensidade 40 N sobre um corpo de massa igual a 4 kg, para que sua velocidade passe de 20 m/s para 40 m/s, na mesma direção e no mesmo sentido.
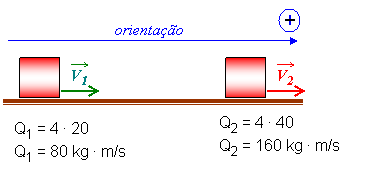
 =
=  2 -
2 -  1I = 160 - 80
1I = 160 - 80
F · Dt = 80
40 · Dt = 80 Dt = 6 s

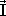 =
= 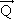 1 -
1 - 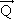 2
2
40 = m.v2 - m.v1
40 = 2 · v2 v2 = 20 m/s
v2 = 20 m/s

7) Sobre uma partícula de 8 kg, movendo-se à 25 m/s, passa a atuar uma força constante de intensidade 2,0.102 N durante 3 s no mesmo sentido do movimento. Determine a quantidade de movimento desta partícula após o término da ação da força.
8) Quanto tempo deve agir uma força de intensidade 100N sobre um corpo de massa igual a 20kg, para que sua velocidade passe de 5m/s para 15m/s?
Solução:
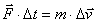
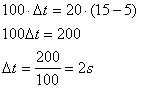
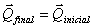
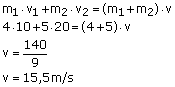 9) Uma bola de tênis, de massa m=200 g e velocidade v1=10 m/s, é rebatida por um jogador, adquirindo uma velocidade v2 de mesmo valor e direção que v1, mas de sentido contrário.
9) Uma bola de tênis, de massa m=200 g e velocidade v1=10 m/s, é rebatida por um jogador, adquirindo uma velocidade v2 de mesmo valor e direção que v1, mas de sentido contrário.
a) Qual foi a variação da quantidade de movimento da bola?
b) Supondo que o tempo de contato da bola com a raquete foi de 0,01 s, qual o valor da força que a raquete exerceu sobre a bola (admitindo que esta força seja constante)?

![]()
![]() =
= 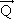 1 -
1 - 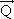 2 40 = m.v2 - m.
2 40 = m.v2 - m.v1 40 = 2 · v2  v2 = 20 m/s11) Leia atentamente as afirmativas abaixo e marque a única opção CORRETA.
v2 = 20 m/s11) Leia atentamente as afirmativas abaixo e marque a única opção CORRETA.
a) A quantidade de movimento Q é uma grandeza escalar.
b) A quantidade de movimento Q é uma grandeza vetorial e seu sentido é o mesmo da aceleração.
c) O impulso I é uma grandeza escalar.
d) O impulso I é uma grandeza vetorial e seu sentido é o mesmo da força que o provoca.
 , definição de Impulso, vetorial, que mostra que seu sentido acompanha o da
, definição de Impulso, vetorial, que mostra que seu sentido acompanha o da
Força, já que ?t é sempre positivo. Letra D.
12) Considere uma situação comum do trânsito: uma criança de 20 Kg, sentada no banco da frente, sendo ?arremessada? contra o pára-brisa durante uma colisão frontal a uma velocidade relativamente baixa de 72 Km/h (20 m/s). A criança pára após o choque.
a) Calcule o módulo do Impulso aplicado sobre esta criança.
b) Se a força de contato entre a criança e o pára-brisa durasse apenas 0,02 s, qual seria o valor então desta força? Entenda, após os cálculos, porque deve-se usar o cinto de segurança e as crianças devem viajar na cadeirinha apropriada, no banco de trás...
Solução:
a) Temos I = ?Q= m . v ? m . v0 , e v=0, pois a criança pára após o choque.
Assim, I = 20.20 = - 400 N.s , onde o sinal de menos indica que o Impulso foi contrário ao
movimento da criança, claro!
b) De I = F.t temos F = t / I F = ?F= 400 / 2 / 100 = 20.000N , ou seja, 2 Toneladas-Força! É por isto que machuca tanto!
13) (UFV) considere uma colisão inelástica de corpos na ausência de forças externas. Com relação à
energia mecânica e à quantidade de movimento (momento linear), é correto afirmar que:
a) ambas se conservam.
b) apenas a energia mecânica se conserva.
c) ambas não se conservam.
d) apenas a quantidade de movimento se conserva
Solução:
O conceito de colisão inelástica é de que há perda de energia mecânica, mas a quantidade de movimento
se conserva.
14) . Um tijolo de massa m igual a 1 Kg é abandonado do repouso, em queda livre. Considere g = 10 m/s²
.
Após 2 segundos de queda, podemos afirmar que sua Quantidade de Movimento Q:
a) vale 20 Kg.m/s, é horizontal e para a direita.
b) vale 2 Kg.m/s, é vertical e para cima.
c) vale 10 Kg.m/s, é horizontal e para a esquerda.
d) vale 20 Kg.m/s, é vertical e para baixo
Solução:
Quem cai, em queda livre, tem velocidade para baixo. O vetor Quantidade de Movimento
? ?
Q = m. v acompanha o sentido da velocidade, e isto já levaria à resposta. Calculando seu módulo e
lembrando que, neste caso, V=gt, t=2s, temos V=2.10=20m/s.
Q = m .v = 1.20 = 20 Kg.m/s
15) . Um corpo de massa m = 3 Kg executa um Movimento Circular Uniforme no sentido anti-horário a
uma velocidade de v = 60 m/s. O módulo, a direção e o sentido do Vetor Quantidade de Movimento
?
Q no ponto P são, respectivamente:
a) 180 Kg.m/s, inclinado e para sudeste.
b) 180 Kg.m/s, inclinado e para noroeste.
c) 20 Kg.m/s, horizontal e para a direita.
d) 20 Kg.m/s, horizontal e para a esquerda.
Solução:
Quanto ao módulo, apenas fórmula:
Q = m . v = 3.60 = 180 Kg.m/s.
A velocidade e a quantidade de movimento são tangentes à trajetória.
16) (UnB-DF) Uma bola de tênis de 100g foi jogada contra uma parede, atingindo-a com velocidade horizontal de 4m/s. Imediatamente após o choque, a bola retornou com velocidade de 3m/s, na mesma direção. Com base nessas informações podemos afirmar que o impulso aplicado pela parede e a energia perdida durante o choque foram respectivamente iguais a:
a) 0,35 N.s e 0,7 J
b) 30 N.s e 0,1 J
c) 0,7 N.s e 0,35 J
d) 0,3 N.s e 0,05 J
e) 0,5 N.s e 0,3 J
17) Em um ponto material é aplicada uma força de intensidade 5,4 x 102 N, durante um intervalo de tempo igual a 1,1 x 10-1s. Determine a intensidade do impulso da força aplicada no ponto material.
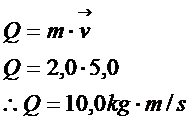
A direção do vetor quantidade de movimento é o mesmo da velocidade. (horizontal)
O sentido do vetor quantidade de movimento é da esquerda para a direita.
a) 1,5 N.s
b) 3,0 N.sc) 6,0 N.s
d) 9,0 N.s
e) 15,0 N.s
22) A figura ilustra uma bola A, com velocidade v, a ponto de colidir com outra bola B que, por sua vez, colidirá com uma terceira bola C. Considerando as bolas de mesma massa e as colisões frontais e elásticas, as velocidades vA, vB e vC de A, B e C, imediatamente após as colisões, serão:
Fontes: aulasparticulares.org/material-de-apoio/fisica/mecanica/impulso-e-quantidade-de-movimento
educar.sc.usp.br/sam/quantidade_movimento_roteiro.html
www.cefetsp.br/edu/okamura/impulso_exercicios_resolvidos.htm
www.mundoeducacao.com/fisica/impulso-quantidade-movimento.htm
- Corrente Elétrica
Os aparelhos eletroeletrônicos que se encontram nas residências precisam de energia elétrica para o seu funcionamento. Tal energia é obtida quando eles são ligados em alguma fonte de energia, como uma pilha ou uma tomada. Quando isso é...
- Momento De Uma Força (torque) - Resumo (com Questões)
Momento de Uma Força (Torque) O conceito de momento (ou torque) é usado, mesmo intuitivamente, com grande frequência em nossa vida diária. É o caso, por exemplo, de uma pessoa que fecha uma porta aplicando a força no meio da porta; obterá um...
- Questões De Vestibular Sobre Energia Potencial Gravitacional E Elástica
Artigo com resumo e questões de vestibulares resolvidas sobre Energia Potencial Gravitacional, Energia Potencial Elástica e Princípio da Conservação da Energia Mecânica Energia Potencial Gravitacional É uma forma de energia...
- Lançamento Vertical E Queda Livre - Resumo (com Questões Resolvidas)
Lançamento Vertical e Queda LivreDenomina-se Queda Livre o movimento vertical, próximo à superfície da Terra, quando um corpo de massa m é abandonado no vácuo ou em uma região onde desprezamos a resistência do ar.A queda livre é um movimento...
- Movimento Uniforme (mu) E Movimento Uniformemente Variado (muv) - Resumo (com Questões)
Definição de movimento uniforme A tartaruga é um bicho estranho. Pode o mundo cair ao seu redor que ela continua se movimentando sem alterar a sua velocidade. Depois que ela sai do repouso e entra em movimento, ela dificilmente varia sua velocidade...
Vestibular
Impulso e Quantidade de Movimento de um Sistema - resumo
Definição de Impulso de uma força. Métodos para calcular o impulso de uma força constante e variável e a quantidade de movimento, com exemplos e exercícios resolvidos.
Impulso e quantidade de movimento
Impulso de Força Constante
Dizemos que uma força produz um impulso sobre um corpo quando ela age no corpo durante um certo intervalo de tempo.
O impulso da força (I) consiste no produto entre a intensidade da força (F) considerada num determinado intervalo de tempo (?t). Dessa maneira, observe abaixo:

OBSERVAÇÃO:
- O impulso é uma grandeza vetorial que possui a mesma direção e mesmo sentido da força atuante.

No Sistema Internacional (SI), a unidade da grandeza impulso é N · s (newton vezes segundo). Como
N = kg · m/s2, temos:

Exemplo :
Sob a ação de uma força resultante constante de intensidade 20N, um corpo, de 1,0kg, parte do repouso no instante t = 0. Calcule o módulo do impulso da resultante, desde t = 0 até t = 5,0s, e a velocidade final.
Solução:
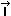 =
=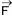
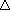 t
t
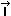 =
=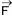
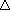 t
tI = 20 . 5 = 100Ns
Para calcular a velocidade, lembre-se de que
v = vo + at, sendo vo = 0 e a = F/m:
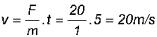
Impulso de Força Variável
Se uma força tiver direção constante e intensidade variando no decorrer do tempo, seu impulso será calculado por meio da área sob o gráfico força × tempo.

Nesse caso, podemos definir uma força média como sendo a força constante capaz de produzir o mesmo impulso da força de intensidade variável. Isto é:

Quantidade de Movimento ou momento linear
Se um corpo de massa m descreve um movimento, numa determinada trajetória, com velocidade v, pode-se dizer que a quantidade de movimento ou momento linear deste corpo é igual ao produto entre a sua massa e sua velocidade. Portanto:

Como a quantidade de movimento é uma grandeza vetorial, apresenta módulo, direção e sentido, temos:

De acordo com o SI, a quantidade de movimento tem como unidade
kg · m/s (quilograma vezes metro por segundo).
Repare que a unidade de quantidade de movimento coincide com a de impulso, embora sejam grandezas diferentes.
Demonstração do Teorema do Impulso
Considere uma partícula de massa (m) constante, em movimento retilíneo uniformemente variado (MRUV).
De acordo com a 2a lei de Newton, a força resultante relaciona-se com a mudança de velocidade da partícula, num certo intervalo de tempo, assim:

Ou seja:



Embora tenhamos demonstrado o Teorema do Impulso a partir de uma situação simples de MRUV, sua aplicação é geral, estendendo-se a qualquer tipo de movimento, sob a ação de forças constantes ou variáveis.
Pode-se, através do que foi apresentado, concluir que as unidades de medida do impulso (N.s) e da quantidade de movimento (kg.m/s) são equivalentes.
Quantidade de Movimento de um Sistema
A quantidade de movimento (ou momento linear) de um conjunto de partículas corresponde à soma vetorial das quantidades de movimento de cada partícula de tal sistema.
Considere, por exemplo, o conjunto formado por três partículas (A, B e C), abaixo indicadas, em que se destaca o vetor quantidade de movimento ( = m · ) que cada uma apresenta em um certo instante.

Obtemos o vetor quantidade de movimento do sistema
( sist), nesse instante, pela seguinte adição vetorial:

Se as velocidades das partículas tivessem a mesma direção, poderíamos obter o valor da quantidade de movimento do sistema através das velocidades escalares das partículas assim:

Sistema Isolado
Em um sistema podem agir forças internas e externas. São chamadas de forças internas aquelas que são trocadas entre as partículas do sistema. Por constituírem pares ação-reação, o impulso total devido às forças internas sempre será nulo.
Uma força é classificada como externa quando é exercida no sistema pelo meio externo a ele. Essa força pode ser de ação a distância (força de campo) ou de contato.
Dizemos que um sistema de partículas é mecanicamente isolado quando for nulo o impulso total das forças externas sobre as partículas do sistema. Ou seja, o sistema será considerado isolado quando:
a) nenhuma força externa atuar, ou a resultante das forças externas for nula;
b) as forças externas forem desprezíveis, se comparadas com as forças internas;
c) a interação com o meio externo tiver uma duração muito pequena ( 0).
Todos os fatores acima nos permitem, portanto, eleger como sistemas isolados usuais os conjuntos de partículas associados aos fenômenos de colisão e explosão.
Por exemplo, observe abaixo a separação de massas (explosão) que uma mola inicialmente comprimida consegue produzir, quando interposta entre dois carrinhos (A e B) dispostos num plano horizontal liso.

Note que no conjunto (A + B + mola) as forças elásticas internas ( e ? ) são as que produzem a separação de A e B, enquanto as forças externas (pesos e normais) têm resultante nula. Logo, temos um sistema isolado.
Relação entre impulso e quantidade de movimento
Vimos que o impulso é dado por:
I = F  t 10.3
t 10.3
 t 10.3
t 10.3A força F vai imprimir uma aceleração à bola, a, fazendo que a sua velocidade altere de um valor inicial V1, para um valor V2.
A força F é calculada pela 2a Lei de Newton:
A força F é calculada pela 2a Lei de Newton:
F = m a 10.4
Substituindo 10.4 em 10.3, temos:
I = m a  t 10.5
t 10.5
 t 10.5
t 10.5Como a =  V /
V /  t , substituindo na expressão 10.5:
t , substituindo na expressão 10.5:
 V /
V /  t , substituindo na expressão 10.5:
t , substituindo na expressão 10.5:I = m ( V /
V /  t) /
t) /  t = m
t = m  V = m (V 2- V1) = m V 2- m V1
V = m (V 2- V1) = m V 2- m V1
 V /
V /  t) /
t) /  t = m
t = m  V = m (V 2- V1) = m V 2- m V1
V = m (V 2- V1) = m V 2- m V1Como Q = m V (10.2), substituindo, obtemos que:
I = Q 2- Q1 10.6
A equação 10.5 mostra que o impulso, exercido por uma força ou por uma resultante de forças, em um intervalo de tempo, é igual à variação da quantidade de movimento.
Conservação da Quantidade de Movimento
Você já deve ter visto em colisões de curta duração como por exemplo com bolas em um jogo de bilhar, dependendo da direção e sentido do impulso que for dado à bola com taco, após o choque com uma bola de bilhar em repouso na mesa, as bolas podem se movimentar em quaisquer direções e sentidos.
Vamos analisar o caso mais simples em que bolas de massas diferentes, movimentando-se na em sentidos opostos (fig. 10.2a), após a colisão, se movimentam na mesma direção e mesmo sentido (fig. 10.2b).
 |  |
(a) (b)
Consideremos como dados:
mA = 4 kg
mB= 2 kg
Medindo os valores das velocidades antes e depois da colisão, foram obtidos os seguintes valores experimentalmente:
mB= 2 kg
Medindo os valores das velocidades antes e depois da colisão, foram obtidos os seguintes valores experimentalmente:
| Bola A | Bola B | |
| Antes da colisão | V 1A = 6 m/s | V1B = 4 m/s |
| Depois da colisão | V 2A = 1 m/s | V2B = 6 m/s |
Calculando a quantidade de movimento antes da colisão:
Q1 = mA V 1A- mBV1B=4 x 6 - 2 x 4 = 24 - 8 = 16 kg m/s
Observe que como os vetores quantidades de movimentos têm sentidos contrários foi realizada a diferença entre os módulos dos dois vetores.
Calculando a quantidade de movimento depois da colisão:
Q2 = mAV 2A+mBV2B = 4 x 1 + 2 x 6 = 16 kg m/s
Chegamos à conclusão que:
Q1 = Q2
ou seja, as quantidades de movimento se conservam.
Por quê?
Quando houve a colisão das bolas, considerando que o sistema seja isolado de forças externas (forças externas nulas), ou se
a resultante das forças externas fôr nula, o impulso é nulo:
Considerando a expressão 10.6:
a resultante das forças externas fôr nula, o impulso é nulo:
Considerando a expressão 10.6:
I = Q1 + Q2
Como pela expressão 10.3:
I = F  t = 0 x
t = 0 x  t = 0
t = 0
 t = 0 x
t = 0 x  t = 0
t = 0onde F é a resultante das forças externas.
Substituindo, obtemos:
Q1 + Q2 = 0
que é o Princípio da Conservação da Quantidade de Movimento:
"É constante a quantidade de movimento de um sistema quando a resultante das forças externas for nula".
Qinicial = Qfinal 10.7
sendo as quantidades de movimento grandezas vetoriais.
Vamos ver se você entendeu.
Considere um carro pequeno com massa 500 kg com velocidade de 20 m/s e um caminhão com massa 3000 kg com velocidade também de 20 m/s, que estão se movimentando em sentidos contrários (10.3). Em um determinado instante, eles colidem frontalmente. Pergunto: o carro exerce força maior sobre o caminhão ou vice-versa?

Figura 1.1 - Carro e caminhão se movimentando em sentidos contrários, mesma direção e com velocidades iguais
Se você respondeu que o caminhão exerceu maior força sobre o carro, errou! Porque as forças são iguais em módulo e atuam em corpos diferentes (3a Lei de Newton).
Mas você pode perguntar: por quê o carro ficou mais danificado que o caminhão? Para você ter a resposta calcule a quantidade de movimento antes do choque. Você vai verificar que a quantidade de movimento do caminhão antes do choque é maior que a quantidade de movimento do carro, provocando maior estrago no carro. Entendeu?
Temos outras situações em que a conservação da quantidade de movimento se conserva:
- Na distensão ou compressão de uma mola existente entre dois blocos.
Quando distendemos ou comprimimos a mola, exercemos uma força externa F. Ao liberarmos a mola ela volta para a sua posição inicial. Como?
Quando a mola é deformada, ao aplicarmos a força externa F (força de tração T no exemplo), temos que vai aparecer uma força na mola que atua no sentido contrário ao da força aplicada F, intrínseca à mola denominada força elástica, Fel. Quando é retirada a força externa F, é a força elástica Fel que faz com que a mola volte para sua posição inicial. Neste caso vale o princípio da conservação da quantidade de movimento porque a resultante das forças externa é nula (fig. 10.4).

Figura 1.2 - Dois blocos A e B ligados por uma mola
Inicialmente o sistema está em repouso, portanto a quantidade de movimento incial é nula:
Qinicial = 0
Quando é retirada a força externa F, o bloco A se desloca com com VA e o bloco B com velocidade VB. A quantidade de movimento final é:
Qfinal = m A VA - m B VB
Qinicial = Qfinal
0 = m A VA - m B VB
m A VA = m B VB
- Em um jogo de bilhar, a quantidade de movimento também se conserva.
Após a colisão as bolas podem ter diferentes sentidos e direções (fig.10.5).
 |  |
Aplicando o princípio da conservação da quantidade de movimento, na direção x, temos:
Qinicialx = Qfinalx
m A V1Ax = m B V2B x+ m A V2Ax
m A V1A = m B V2B cos  B+ m A V2A cos
B+ m A V2A cos  A
A
 B+ m A V2A cos
B+ m A V2A cos  A
ANa direção y, temos:
Q (inicial)y = Q(final)y
0 = m B V2By - m A V2Ay
0 = m B V2Bsen  B - m A V2A sen
B - m A V2A sen  A
A
 B - m A V2A sen
B - m A V2A sen  A
AColisões Frontais
Neste módulo, trataremos da mecânica relacionada às colisões frontais de partículas. A colisão entre dois corpos é denominada frontal ou unidimensional quando não ocorre mudança na direção da velocidade desses corpos, ou seja, as velocidades dos corpos, antes e depois do choque, possuem a mesma direção.
Sabemos que nas colisões há conservação da quantidade de movimento do sistema. Isto é: no choque entre duas partículas A e B, as quantidades de movimento de cada partícula variam, mas a quantidade de movimento do sistema se conserva.

Para um choque frontal, podemos escrever a equação de conservação de quantidade de movimento do sistema usando velocidades escalares, ou seja, atribuindo um sinal algébrico às velocidades das partículas de acordo com a orientação (positiva) definida para a trajetória.

Coeficiente de Restituição
Embora sempre ocorra a conservação da quantidade de movimento do sistema, numa colisão pode ou não haver conservação de energia mecânica do sistema.
Os choques são classificados em função da conservação ou não da energia cinética do sistema. Quando a energia cinética do sistema imediatamente após o choque é igual à energia cinética do sistema imediatamente antes do choque, ele recebe o nome de choque perfeitamente elástico. Se as energias cinéticas do sistema antes e após o choque forem diferentes, ele recebe o nome de choque não-elástico.
Tais denominações foram originadas em experiências com choques frontais entre um móvel e um anteparo rígido (uma parede, por exemplo).
Suponha que um carrinho se aproxime frontalmente de uma parede a 10 m/s e, após o choque, se afaste desta com velocidade de módulo 6 m/s.

Após o choque, o carrinho tem restituída apenas 60% da velocidade, em módulo, que possuía antes do choque. Conclusão: houve perda de energia cinética nessa colisão.
A partir disso, criou-se um coeficiente de restituição (e) para as colisões frontais, definido pela razão entre o módulo da velocidade de afastamento (após o choque) e o módulo da velocidade de aproximação (antes do choque).

Caso ocorresse 100% de restituição do módulo da velocidade (vafast. = vaprox.), o coeficiente de restituição atingiria seu valor máximo (e = 1) e não haveria perda de energia mecânica. Esse choque, denominado perfeitamente elástico, pode ser simulado lançando-se o carrinho contra uma mola ideal fixa numa parede, como mostra a figura abaixo.

Entre os choques não-elásticos, destaca-se o choque perfeitamente inelástico, no qual se produz a maior perda de energia mecânica. Este choque ocorre quando o coeficiente de restituição é mínimo, ou seja, igual a zero (e = 0). Num choque desse tipo, o carrinho lançado contra a parede não retornaria (grudar-se-ia nesta) e, por conseguinte, perderia toda sua energia mecânica inicial.
Sintetizando, podemos comparar os tipos de choques frontais assim:

Para estendermos a definição de coeficiente de restituição para uma colisão entre duas partículas
(A e B), basta que usemos velocidade relativa, ou seja, que tomemos a velocidade que uma partícula possui em relação à outra (eleita como ?parede?).
(A e B), basta que usemos velocidade relativa, ou seja, que tomemos a velocidade que uma partícula possui em relação à outra (eleita como ?parede?).

Dessa forma, o coeficiente de restituição será obtido pela razão entre as velocidades relativas, depois e antes do choque, assim:

Questões resolvidas sobre Impulso e Quantidade de Movimento
1) Ao dar um chute na bola, num jogo de futebol, um jogador aplica um força de intensidade 6,0 · 10² N sobre a bola, durante um intervalo de tempo de 1,5 · 10-1 s. Determine a intensidade do impulso da força aplicada pelo jogador.
SOLUÇÃO:
Dados do enunciado
F = 6,0 · 10² N
t = 1,5 · 10-1 s
t = 1,5 · 10-1 s
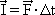
 I = 90 N.s
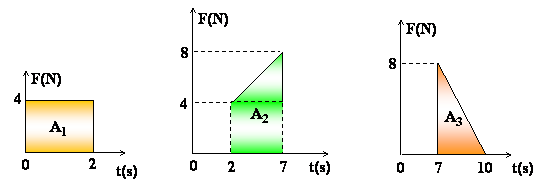
I = 90 N.s2) Dado o gráfico

Determine:
a) o módulo da força no intervalo de tempo de 0 s a 10 s.
b) a intensidade da força constante que produz o mesmo impulso que a força dada no intervalo de 0 s a 10 s.
a) o módulo da força no intervalo de tempo de 0 s a 10 s.
b) a intensidade da força constante que produz o mesmo impulso que a força dada no intervalo de 0 s a 10 s.
SOLUÇÃO:
1. Divida o gráfico em 3 partes: triângulo (A3), retângulo (A1) e trapézio (A2).

2. Calcule as áreas A1, A2 e A3.
A1 = b · h  A1 = 2s · 4N = 8 N.s
A1 = 2s · 4N = 8 N.s
A2 =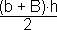
 A2 =
A2 = 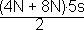 = 30 N.s
= 30 N.s
A3 =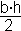
 A3 =
A3 = 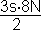 = 12 N.s
= 12 N.s
 A1 = 2s · 4N = 8 N.s
A1 = 2s · 4N = 8 N.sA2 =
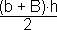
 A2 =
A2 = 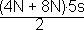 = 30 N.s
= 30 N.sA3 =
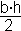
 A3 =
A3 = 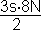 = 12 N.s
= 12 N.s 3. A soma de A1, A2 e A3 é o valor do impulso.
I = A1+ A2 + A3  I = 50 N.s
I = 50 N.s
 I = 50 N.s
I = 50 N.s 4. Determine a força utilizando 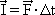
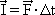
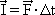
 F =
F =  = 5 N
= 5 N3) Determine durante quanto tempo deve agir uma força de intensidade 40 N sobre um corpo de massa igual a 4 kg, para que sua velocidade passe de 20 m/s para 40 m/s, na mesma direção e no mesmo sentido.
PROCEDIMENTOS:
1. Represente sobre o corpo a direção e o sentido das velocidades;
2. Adote uma orienração;
3. Aplique Q = m · v, para cada velocidade, observando a orientação adotada;
4. Determine o tempo gasto utilizando I = F · Dt.
2. Adote uma orienração;
3. Aplique Q = m · v, para cada velocidade, observando a orientação adotada;
4. Determine o tempo gasto utilizando I = F · Dt.
SOLUÇÃO:

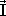 =
= 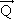 2 -
2 - 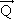 1I = 160 - 80
1I = 160 - 80F · Dt = 80
40 · Dt = 80 Dt = 6 s
4) O gráfico abaixo mostra a variação da intensidade da força 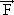 , de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
, de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
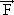 , de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
, de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
PROCEDIMENTO:
1. Calcule a área do triângulo (representa o impulso);
2. Use o teorema do impulso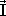 =
= 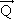 2 -
2 - 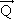 1, e determine a velocidade
1, e determine a velocidade
2. Use o teorema do impulso
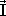 =
= 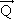 2 -
2 - 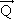 1, e determine a velocidade
1, e determine a velocidadeSOLUÇÃO:
I = 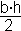
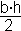
I = 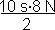
 I = 40 N.s
I = 40 N.s
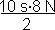
 I = 40 N.s
I = 40 N.s =
=  1 -
1 - 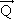 2
240 = m.v2 - m.
40 = 2 · v2
 v2 = 20 m/s
v2 = 20 m/s5) Um corpo de massa 0,5 kg cai em queda livre. Considerando g = 10 m/s², dê as características do impulso do peso do corpo durante 4 segundo de queda.
SOLUÇÃO:
Dados do enunciado
m = 0,5 kg
g = 10 m/s² Dt = 4 s
g = 10 m/s² Dt = 4 s
Módulo: I = mg·Dt = 0,5 · 10 · 4 = 20 N.s
Direção: Vertical
Sentido: Para baixo
Direção: Vertical
Sentido: Para baixo
6) (FMTM) Um projétil de aço de massa 40 g é atirado horizontalmente contra um bloco de argila de massa 160 g, inicialmente em repouso, suspenso por fios inextensíveis e de massas desprezíveis, conforme mostra a figura. O projétil penetra o bloco e o sistema projétil bloco se eleva, atingindo altura máxima igual à 5 cm. Considerando o sistema conservativo (sistema no qual não há perda de energia) e g = 10 m/², a velocidade do projétil ao atingir o bloco de argila era, em m/s, igual a:

Solução:
mp = 40g = 0,04kg
mb = 160g = 0,16kg
h = 5cm = 0,05m
g = 10m/s²
vp = ?
mb = 160g = 0,16kg
h = 5cm = 0,05m
g = 10m/s²
vp = ?
O momento antes do choque é igual ao momento posterior ao choque.
Qa = Qd
vp.mp + vb.mb = vpb.(mp + mb)
vp.0,04 + 0 = vpb.(0,04 + 0,16)
vpb = 0,04vp / 0,2 - equação I
vp.mp + vb.mb = vpb.(mp + mb)
vp.0,04 + 0 = vpb.(0,04 + 0,16)
vpb = 0,04vp / 0,2 - equação I
Como o sistema é conservativo, a energia mecânica é conservada.
Ema = Emd
Eca = Epd
m.vpb2 / 2 = m.g.h
Eca = Epd
m.vpb2 / 2 = m.g.h
vpb = (2.g.h)1/2 - equação II
Igualando as equações I e II
0,04vp / 0,2 = (2.g.h)1/2
vp = 0,2.(2.10.0,05)1/2/0,04
vp = 0,2/0,04
vp = 5m/s
vp = 0,2.(2.10.0,05)1/2/0,04
vp = 0,2/0,04
vp = 5m/s
7) Sobre uma partícula de 8 kg, movendo-se à 25 m/s, passa a atuar uma força constante de intensidade 2,0.102 N durante 3 s no mesmo sentido do movimento. Determine a quantidade de movimento desta partícula após o término da ação da força.
Solução:
O impulso pode ser definido como a variação da quantidade de movimento:
I = Q2 ? Q1
F.?t = Q2 ? Q1
2.102.3 = Q2 ? 25.8
Q2 = 600 + 200
Q2 = 800 kgm/s
I = Q2 ? Q1
F.?t = Q2 ? Q1
2.102.3 = Q2 ? 25.8
Q2 = 600 + 200
Q2 = 800 kgm/s
Solução:
8) Um corpo de massa 4kg, se desloca com velocidade constante igual a 10m/s. Um outro corpo de massa 5kg é lançado com velocidade constante de 20m/s em direção ao outro bloco. Quando os dois se chocarem ficarão presos por um velcro colocado em suas extremidades. Qual será a velocidade que os corpos unidos terão?
Solução:
a) Qual foi a variação da quantidade de movimento da bola?
b) Supondo que o tempo de contato da bola com a raquete foi de 0,01 s, qual o valor da força que a raquete exerceu sobre a bola (admitindo que esta força seja constante)?
Solução:
a) Para iniciar a resolução é necessário lembrar que no SI utilizamos o Kg, então a massa do corpo será m = 0,2 kg.
O valor de sua quantidade de movimento no instante em que a bola atinge a raquete é:
Q1 = m.v1
Q1 = 0,2 . 10
Q1 = 2kg.m/s
No instante em que ela abandona a raquete, sua quantidade de movimento vale:
Q2 = m.v2
Q2 = 0,2.10
Q2 = 2kg.m/s
Lembrando que Q1 e Q2 são vetores, eles têm a mesma direção e sentidos opostos. Adotando o sentido de ida da bola como sendo negativo e o sentido contrário como positivo, podemos afirmar que a quantidade de movimento da bola variou de -2kg.m/s para +2kg.m/s, logo a variação da quantidade de movimento é dada por:
?Q = Q2 ? Q1
?Q = 2 ? (-2)
?Q = 2 + 2
?Q = 4kg.m/s
b) O impulso I =F. ?t que a raquete exerceu na bola é igual a variação da quantidade de movimento.
F. ?t = ?Q
F.0,01 = 4
F = 4 / 0,01
F = 400N
F = 4. 102 N
O valor de sua quantidade de movimento no instante em que a bola atinge a raquete é:
Q1 = m.v1
Q1 = 0,2 . 10
Q1 = 2kg.m/s
No instante em que ela abandona a raquete, sua quantidade de movimento vale:
Q2 = m.v2
Q2 = 0,2.10
Q2 = 2kg.m/s
Lembrando que Q1 e Q2 são vetores, eles têm a mesma direção e sentidos opostos. Adotando o sentido de ida da bola como sendo negativo e o sentido contrário como positivo, podemos afirmar que a quantidade de movimento da bola variou de -2kg.m/s para +2kg.m/s, logo a variação da quantidade de movimento é dada por:
?Q = Q2 ? Q1
?Q = 2 ? (-2)
?Q = 2 + 2
?Q = 4kg.m/s
b) O impulso I =F. ?t que a raquete exerceu na bola é igual a variação da quantidade de movimento.
F. ?t = ?Q
F.0,01 = 4
F = 4 / 0,01
F = 400N
F = 4. 102 N
10) O gráfico abaixo mostra a variação da intensidade da força 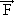 , de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
, de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
 , de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
, de direção constante, que atua sobre um objeto de massa m = 2,0 kg. Sendo para t = 0 s, v0 = 0 m/s, determine sua velocidade em t = 10 s.
Solução:
I![]()
![]() =
= 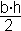 I =
I = 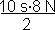 I = 40 N.s
I = 40 N.s

 =
= 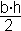 I =
I = 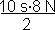 I = 40 N.s
I = 40 N.s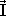

 =
= 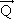 1 -
1 - 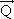 2 40 = m.v2 - m.
2 40 = m.v2 - m. v2 = 20 m/s
v2 = 20 m/sa) A quantidade de movimento Q é uma grandeza escalar.
b) A quantidade de movimento Q é uma grandeza vetorial e seu sentido é o mesmo da aceleração.
c) O impulso I é uma grandeza escalar.
d) O impulso I é uma grandeza vetorial e seu sentido é o mesmo da força que o provoca.
Solução:
 , definição de Impulso, vetorial, que mostra que seu sentido acompanha o da
, definição de Impulso, vetorial, que mostra que seu sentido acompanha o da Força, já que ?t é sempre positivo. Letra D.
12) Considere uma situação comum do trânsito: uma criança de 20 Kg, sentada no banco da frente, sendo ?arremessada? contra o pára-brisa durante uma colisão frontal a uma velocidade relativamente baixa de 72 Km/h (20 m/s). A criança pára após o choque.
a) Calcule o módulo do Impulso aplicado sobre esta criança.
b) Se a força de contato entre a criança e o pára-brisa durasse apenas 0,02 s, qual seria o valor então desta força? Entenda, após os cálculos, porque deve-se usar o cinto de segurança e as crianças devem viajar na cadeirinha apropriada, no banco de trás...
Solução:
a) Temos I = ?Q= m . v ? m . v0 , e v=0, pois a criança pára após o choque.
Assim, I = 20.20 = - 400 N.s , onde o sinal de menos indica que o Impulso foi contrário ao
movimento da criança, claro!
b) De I = F.t temos F = t / I F = ?F= 400 / 2 / 100 = 20.000N , ou seja, 2 Toneladas-Força! É por isto que machuca tanto!
13) (UFV) considere uma colisão inelástica de corpos na ausência de forças externas. Com relação à
energia mecânica e à quantidade de movimento (momento linear), é correto afirmar que:
a) ambas se conservam.
b) apenas a energia mecânica se conserva.
c) ambas não se conservam.
d) apenas a quantidade de movimento se conserva
Solução:
O conceito de colisão inelástica é de que há perda de energia mecânica, mas a quantidade de movimento
se conserva.
14) . Um tijolo de massa m igual a 1 Kg é abandonado do repouso, em queda livre. Considere g = 10 m/s²
.
Após 2 segundos de queda, podemos afirmar que sua Quantidade de Movimento Q:
a) vale 20 Kg.m/s, é horizontal e para a direita.
b) vale 2 Kg.m/s, é vertical e para cima.
c) vale 10 Kg.m/s, é horizontal e para a esquerda.
d) vale 20 Kg.m/s, é vertical e para baixo
Solução:
Quem cai, em queda livre, tem velocidade para baixo. O vetor Quantidade de Movimento
? ?
Q = m. v acompanha o sentido da velocidade, e isto já levaria à resposta. Calculando seu módulo e
lembrando que, neste caso, V=gt, t=2s, temos V=2.10=20m/s.
Q = m .v = 1.20 = 20 Kg.m/s
15) . Um corpo de massa m = 3 Kg executa um Movimento Circular Uniforme no sentido anti-horário a
uma velocidade de v = 60 m/s. O módulo, a direção e o sentido do Vetor Quantidade de Movimento
?
Q no ponto P são, respectivamente:
a) 180 Kg.m/s, inclinado e para sudeste.
b) 180 Kg.m/s, inclinado e para noroeste.
c) 20 Kg.m/s, horizontal e para a direita.
d) 20 Kg.m/s, horizontal e para a esquerda.
Solução:
Quanto ao módulo, apenas fórmula:
Q = m . v = 3.60 = 180 Kg.m/s.
A velocidade e a quantidade de movimento são tangentes à trajetória.
16) (UnB-DF) Uma bola de tênis de 100g foi jogada contra uma parede, atingindo-a com velocidade horizontal de 4m/s. Imediatamente após o choque, a bola retornou com velocidade de 3m/s, na mesma direção. Com base nessas informações podemos afirmar que o impulso aplicado pela parede e a energia perdida durante o choque foram respectivamente iguais a:
a) 0,35 N.s e 0,7 J
b) 30 N.s e 0,1 J
c) 0,7 N.s e 0,35 J
d) 0,3 N.s e 0,05 J
e) 0,5 N.s e 0,3 J
Solução:
I = |?Q|
I = |m . (Vf - Vi)|
i = |0,1.(-3 - 4) * por que (-3-4) e não I = 0,1 (3 - 4) ??
I = |0,1.7|
I = 0,7 N.s
I = |m . (Vf - Vi)|
i = |0,1.(-3 - 4) * por que (-3-4) e não I = 0,1 (3 - 4) ??
I = |0,1.7|
I = 0,7 N.s
I = F.tI = m.a.t
I = m. ?v/?t . t
I = m.?v
I = 0,1 . ( -3 - 4) -> adotando um sentido para a velocidade [adotei que está no sentido positivo quando em direção ao encontro da parede]
I = - 0, 7 [em módulo]
Ediss = Ef - E0Ediss = mVf²/2 - mV0²/2
= 0,1 . 9 / 2 - 0,1 . 16 / 2
= 0,45 - 0,80
= - 0,35 J
I = m. ?v/?t . t
I = m.?v
I = 0,1 . ( -3 - 4) -> adotando um sentido para a velocidade [adotei que está no sentido positivo quando em direção ao encontro da parede]
I = - 0, 7 [em módulo]
Ediss = Ef - E0Ediss = mVf²/2 - mV0²/2
= 0,1 . 9 / 2 - 0,1 . 16 / 2
= 0,45 - 0,80
= - 0,35 J
17) Em um ponto material é aplicada uma força de intensidade 5,4 x 102 N, durante um intervalo de tempo igual a 1,1 x 10-1s. Determine a intensidade do impulso da força aplicada no ponto material.
Solução:

18) Seja uma pequena esfera de massa 2,0 kg, que em um determinado instante apresenta uma velocidade horizontal, orientada da esquerda para a direita e de módulo igual a 5,0 m/s. Determine o módulo, a direção e o sentido da quantidade de movimento dessa esfera.
Solução: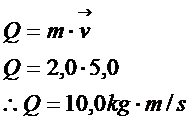
A direção do vetor quantidade de movimento é o mesmo da velocidade. (horizontal)
O sentido do vetor quantidade de movimento é da esquerda para a direita.
19) (Fuvest-SP) Um menino de 40kg está sobre um skate que se move com velocidade constante a 3 m/s numa trajetória retilínea e horizontal. Defronte de um obstáculo ele salta e após 1 s cai sobre o skate, que durante todo o tempo mantém velocidade de 3 m/s.
Desprezando eventuais forças de atrito, calcule:
a) a altura que o menino atingiu no seu salto, tomando como referência a base do skate;
b) a quantidade de movimento do menino no ponto mais alto da sua trajetória.
b) a quantidade de movimento do menino no ponto mais alto da sua trajetória.
Solução:
a) Só por na fórmula da altura.
h = g.t²/2
Se ele demorou 1 segundo para completar tal movimento,então gastou 0,5 para subir e 0,5 para descer,totalizando 1 segundo.então:
h =10*0,5²/2
h =10*0,25/2
h =2,5/2 ------ h=1,25 metros.
h = g.t²/2
Se ele demorou 1 segundo para completar tal movimento,então gastou 0,5 para subir e 0,5 para descer,totalizando 1 segundo.então:
h =10*0,5²/2
h =10*0,25/2
h =2,5/2 ------ h=1,25 metros.
b)?Q = 40*3
?Q = 120 Kg*m/s
20) A bola A, com 1,0 kg de massa, movendo-se à velocidade de 8,0 m/s, choca-se com a bola B, inicialmente em repouso e com massa igual à da bola A. Após a colisão, a bola A move-se perpendicularmente a sua direção original de movimento, como mostra a figura, com velocidade de 6,0 m/s.
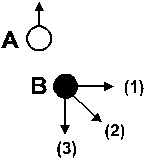
antes da colisão

depois da colisão

Para a bola B, após a colisão, a magnitude e a direção do vetor quantidade de movimento dentre as indicadas por (1) , (2) e (3) são:
Solução:
Vamos resolver por partes:
1) Pra qualquer tipo de colisão podemos dizer que temos conservação da quantidade de movimento, certo?
Assim, temos Qantes = Qdepois
Mas há um detalhe aqui: temos que trabalhar separadamente com os eixos x e y. Então ficamos com duas equações:
Qantes(x) = Qdepois(x)
Qantes(y) = Qdepois(y)
2) Resolvendo, temos:
2.1) Eixo X:
m(a) . v(a) = m(b) . v(b) ou seja, 1 . 8 = 1 . v(b)
Assim, a velocidade do corpo b no EIXO X é 8m/s
2.2) Eixo Y:
0 = m(a) . v(a) - m(b) . v(b) ou seja 0 = 1 . 6 - 1 . v(b)
Assim, a velocidade do corpo b no EIXO Y é 6m/s
3) Como o corpo tem velocidade 8m/s no eixo X e 6m/s no eixo Y, fazendo pitágoras temos uma velocidade de 10m/s inclinada com sentido sudeste (vetor 2).
21) Um projétil de massa 15 g incide horizontalmente sobre uma tábua com velocidade 600 m/s e a abandona com velocidade ainda horizontal de 400 m/s. O impulso comunicado ao projétil pela tábua tem valor, em módulo:
b) 3,0 N.sc) 6,0 N.s
d) 9,0 N.s
e) 15,0 N.s
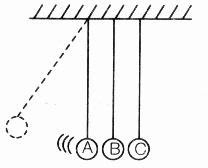
22) A figura ilustra uma bola A, com velocidade v, a ponto de colidir com outra bola B que, por sua vez, colidirá com uma terceira bola C. Considerando as bolas de mesma massa e as colisões frontais e elásticas, as velocidades vA, vB e vC de A, B e C, imediatamente após as colisões, serão:

a) vA = 0 e vB = vC = v/2
b) vA = vB = vC = 0
c) vA = vB = vC = v
d) vA = vB e vC = ve) vA = vB = vC = v/3
b) vA = vB = vC = 0
c) vA = vB = vC = v
d) vA = vB e vC = ve) vA = vB = vC = v/3
23) Um ponto material de massa igual a 10kg possui velocidade constante e igual a 90km/h. Determine a intensidade da quantidade de movimento desse ponto material.
R: I = 250 kg.m/s
24) (UFAL 86) A unidade de quantidade de movimento é:
a) N/s
b) N.m
c) N/kg
d) kg.m/s
e) N.m/s
25) (PUC-SP) Uma bola de tênis, de 100 gramas de massa e velocidade v1 = 20 m/s, é rebatida por um dos jogadores, retornando com uma velocidade v2 de mesmo valor e direção de v1, porém de sentido contrário. Supondo que a força média exercida pela raquete sobre a bola foi de 100 N, qual o tempo contanto entre ambas?
a) zero.
b) 4,0 s.
c) 4,0 x 10-¹ s.
d) 2,0 x 10-² s.
e) 4,0 x 10-² s.
Fontes: aulasparticulares.org/material-de-apoio/fisica/mecanica/impulso-e-quantidade-de-movimento
educar.sc.usp.br/sam/quantidade_movimento_roteiro.html
www.cefetsp.br/edu/okamura/impulso_exercicios_resolvidos.htm
www.mundoeducacao.com/fisica/impulso-quantidade-movimento.htm
- Corrente Elétrica
Os aparelhos eletroeletrônicos que se encontram nas residências precisam de energia elétrica para o seu funcionamento. Tal energia é obtida quando eles são ligados em alguma fonte de energia, como uma pilha ou uma tomada. Quando isso é...
- Momento De Uma Força (torque) - Resumo (com Questões)
Momento de Uma Força (Torque) O conceito de momento (ou torque) é usado, mesmo intuitivamente, com grande frequência em nossa vida diária. É o caso, por exemplo, de uma pessoa que fecha uma porta aplicando a força no meio da porta; obterá um...
- Questões De Vestibular Sobre Energia Potencial Gravitacional E Elástica
Artigo com resumo e questões de vestibulares resolvidas sobre Energia Potencial Gravitacional, Energia Potencial Elástica e Princípio da Conservação da Energia Mecânica Energia Potencial Gravitacional É uma forma de energia...
- Lançamento Vertical E Queda Livre - Resumo (com Questões Resolvidas)
Lançamento Vertical e Queda LivreDenomina-se Queda Livre o movimento vertical, próximo à superfície da Terra, quando um corpo de massa m é abandonado no vácuo ou em uma região onde desprezamos a resistência do ar.A queda livre é um movimento...
- Movimento Uniforme (mu) E Movimento Uniformemente Variado (muv) - Resumo (com Questões)
Definição de movimento uniforme A tartaruga é um bicho estranho. Pode o mundo cair ao seu redor que ela continua se movimentando sem alterar a sua velocidade. Depois que ela sai do repouso e entra em movimento, ela dificilmente varia sua velocidade...
